3 Flokkun vigra¶

Í þessari grein verður fjallað um aðferðir til að flokka (cluster, partition) vigra í hópa (groups) þannig að vigrarnir í hverjum hópi séu líkir hver öðrum, en vigrar í mismunandi hópum séu ekki eins líkir. Verkefni af þessu tagi er nefnt clustering á ensku. Sér í lagi verður farið í hið velþekkta k-means reiknirit (oftast er bara talað um k-means og ekki reynt að þýða). Stundum er talað um að flokka mælingar (observations), punkta, einstaklinga eða hluti, og þegar búið er að flokka má tala um meðlimi í hópum. Orðið einkenni (feature) er oft notað um einstök stök í vigrunum sem eru flokkaðir.

Rétt er að nefna skylda hugtakið classification þar sem unnið er með merkt gögn. Íslenska þýðingin sem hér er notuð, sem sé clustering = flokkun er óheppileg, en mörg orðasöfn í Íðorðabanka Árnastofnunar <https://idordabanki.arnastofnun.is/>`_ þýða clustering með klösun og nota flokkun fyrir enska orðið classification. Classification snýst um vélanám með merktum gögnum (supervised learning) en clustering um vélanám með ómerktum gögnum (*unsupervised learning), eins nánar má lesa um í Fyrirlestrarnótum um aðhvarf.

Fyrirhugað er að breyta orðanotkun í þessum kafla fljótlega. Það bíður aðeins vegna þess að verið er að nota kaflann í kennslu nú (í apríl 2024).

3.1 Dæmi um flokkun tvívíðra vigra¶

Á eftirfarandi mynd er dæmi um flokkun tvívíðra vigra, sem sé punkta í planinu.

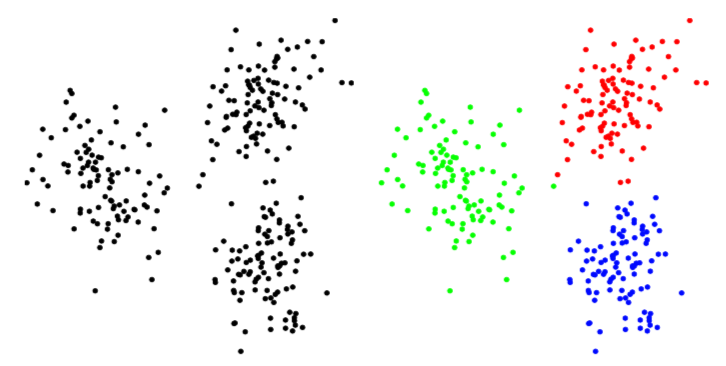
Mynd 3.1: Skipting 300 punkta í þrjá hópa¶

Einn vandi við slíka flokkun er að ákvarða hópafjöldann, sem hefðbundið er að nefna \(k\). Það sem er óvenjulegt við dæmið á myndinni er að vídd punktanna er \(n = 2\) og því er auðvelt að teikna punktasafnið. Í þessu dæmi er líka auðvelt að sjá af myndinni að \(k = 3\) er góð tala, en þetta er ekki svona auðvelt fyrir hærri víddir og jafnvel heldur ekki fyrir önnur tvívíð dæmi.

3.2 Dæmi um hagnýtingu flokkunar¶

Flokkun texta eftir umfjöllunarefni. Hér er nærtækt að taka dæmið um Wikipedia-greinarnar sem voru á dagskrá í Skilaverkefni 7, þar sem unnið var með tíðni 1000 orða í 300 Wikipedia-greinum sem fjölluðu um fimm mismunandi efnisflokka, Pokemon, veðurfræði, listir, stofnanir Sameinuðu þjóðanna, og rafmagnsverkfræði. Góður flokkari ætti að geta fundið (endurskapað) flokkunina, a.m.k. komist nálægt henni útfrá orðtíðnigögnunum einum saman, sérstaklega ef við festum \(k = 5\).

Flokkun sjúklinga. Ef \(x_i\) er vigur af einkennum sjúklings númer \(i\) (t.d. aldur, kyn, BMI, og sjúkdómseinkenni af ýmsu tagi) þá gætti verið gagnlegt að flokka sjúklingana í hópa með svipuð einkenni.

Flokkun viðskiptavina. Gerum ráð fyrir að \(j\)-ta stak \(x_i\) sé magn af vöru \(j\) sem kúnni númer \(i\) keypti á tilteknu tímabili. Þá mætti flokka kúnnana í \(k\) hópa og svo mætti beina sömu auglýsingum til þeirra sem eru í sama hóp, eða t.d. auglýsingum um það sem aðrir í hópnum hafa keypt en þeir ekki.

Auðvelt er að búa til allskonar dæmi af sama tagi: Skipting nemenda í flokka eftir einkunnum og námsbraut (þá mætti t.d. búa til verkefnahópa með einum úr hverjum flokki til að fá fjölbreytni í hópana), flokkun svæða eftir veðurfari, flokkun fyrirtækja eftir ýmsum eiginleikum, o.s.frv.

Í sumum tilvikum er ekkert unnið frekar með flokkana, heldur er tilgangur flokkunarinnar einfaldlega sá að átta sig betur á gagnasafni.

3.3 Ritháttur fyrir flokkun¶

Við látum \(N\) tákna fjölda punkta eða \(n\)-vigra sem á að skipta í \(k\) hópa og látum svo \(G_j\) vera mengi með númerum þeirra punkta sem eru i \(j\)-ta hópnum. Tökum sem dæmi að 7 punktum sé skipt í 3 hópa, með \(x_1\), \(x_3\) og \(x_5\) í fyrsta hópnum, \(x_2\) og \(x_4\) í hópi 2 og \(x_6\) og \(x_7\) í þeim þriðja. Þá verður:

\[G_1 = \{1, 3, 5\},\quad G_2 = \{2, 4\}\quad\text{og}\quad G_3 = \{6, 7\}\]

Við skilgreinum líka vigur \(c\) með \(c_i = {}\) númer hópsins sem \(x_i\) lendir í. Fyrir dæmið okkar verður

\[c = (1, 2, 1, 2, 1, 3, 3)\]

Vigurinn \(c\) svarar til Python-breytunnar code í grein 3.6.

3.4 Miðpunktar hópa¶

Miðpunktur (centroid) fyrir hóp er punktur sem líkist punktunum í hópnum, en hann þarf samt ekki að vera sjálfur í hópnum. Í k-means reikniritinu sem við lýsum nákvæmlega hér að neðan er miðpunktur hóps reiknaður sem meðaltal af öllum punktum í hópnum. Ef \(G_1,\ldots,G_k\) er flokkun \(x_1,\ldots,x_N\) og stærð \(j\)-ta hópsins er \(p_j\) þá má reikna miðpunkta hópanna með:

\[\begin{split}&\textit{Reikna-miðpunkta:}\\[3pt] &\textbf{Fyrir } j = 1,\ldots,k: \\ &\qquad m_j := \frac{1}{p_j} \sum_{i \in G_j}{} x_i\end{split}\]

Í tvívíðu og þrívíðu rúmi þá er miðpunktur reiknaður með þessum hætti sá sami og eðlisfræðileg þungamiðja punktasafnsins. Ef þungir hlutir væru festir á létt (tvívítt) spjald, á staði sem svara til punktasafns, þá mundi spjaldið ballansera á þungamiðjunni. Athugið að fyrir þrívíða punkta t.d. er hægt að láta \(\overline x\), \(\overline y\) og \(\overline z\) vera meðaltöl \(x\)-, \(y\)- og \(z\)-hnita punktanna og þá verður \((\overline x, \overline y, \overline z)\) miðpunkturinn.

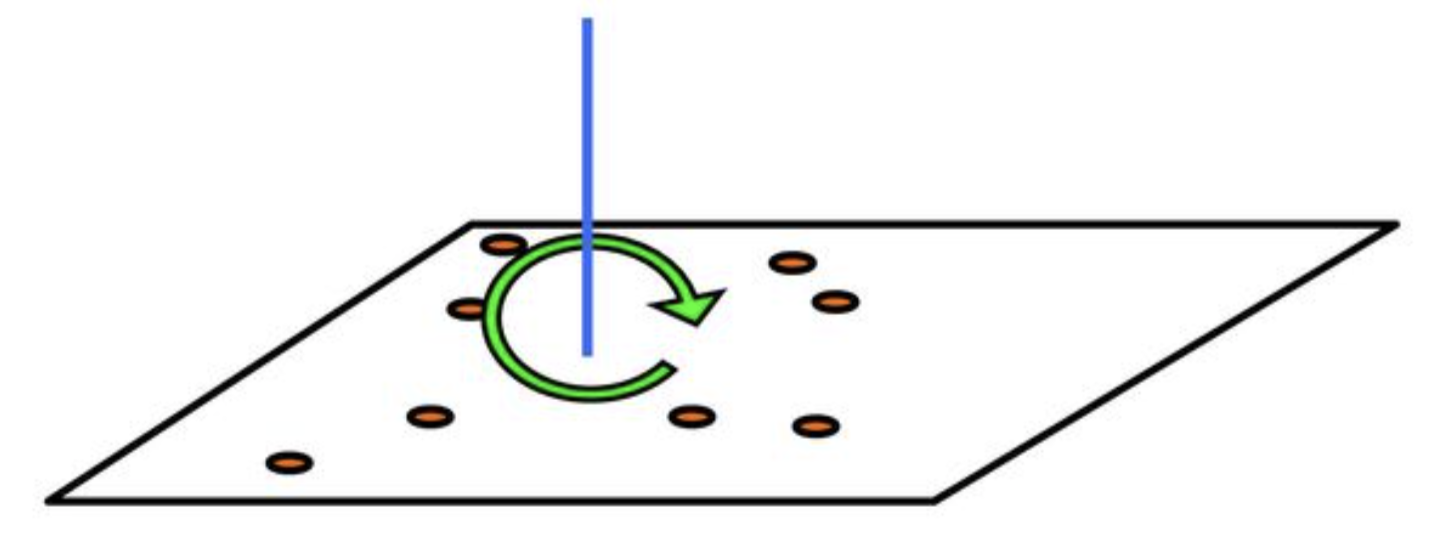
Mynd 3.2: Þungamiðja spjalds með punktmössum¶

Sýnidæmi: Miðpunktur punktasafns

Miðpunktur eða meðaltal \(\{(1,3,4), (2,6,8), (3,6,9)\}\) er \(\frac{1}{3}(1 + 2 + 3, 3 + 6 + 6, 4 + 8 + 9)\) = \(\frac{1}{3}(6,15,21)\) = \((2,5,7)\).

Æfing: Punktar í planinu og miðpunktur þeirra

Finnið miðpunkt fyrir punktana \((1,1), (1,2), (2,4)\) og \((4,5)\). Merkið punktana og meðaltalið inn í hnitakerfi.

3.5 Besta hópaskipting¶

Fyrir \(N\) punkta, \(x_1, \ldots, x_N\) og \(k\) gefna miðpunkta, \(m_1, \ldots, m_k\) er hægt að reikna svokallaða bestu hópaskiptingu með eftirfarandi reikniriti:

\[\begin{split}\DeclareMathOperator*{\argmin}{argmin} &\textit{Besta-skipting:}\\[3pt] &G_h := \varnothing\;\; (h = 1,\ldots, k) \\ &\textbf{Fyrir } i = 1,\ldots,N: \\ &\qquad h := \argmin_{1 \leq j\leq k} \|x_i - m_j\| \\ &\qquad G_h := G_h \cup \{i\}\end{split}\]

Með öðrum orðum finnum við fyrir hvern punkt þann miðpunkt sem er næstur og setjum svo punktinn í tilsvarandi hóp. Stundum eru miðpunktarnir kallaðir fulltrúar og þá má segja að hver einstaklingur lendi í hópi þess fulltrúa sem er líkastur honum. Þetta minnir á kosningapróf sem ýmsir vefmiðlar bjóða í aðdraganda kosninga, þar sem hægt er að finna út hvaða flokk maður ætti að kjósa með því bera svör manns saman við svör frambjóðenda við sömu spurningum.

Æfing: Besta hópaskipting með blaði og blýanti

Merkið 10 punkta af handahófi á blað ásamt 3 miðpunktum og búið til bestu hópaskiptingu.

3.6 k-means reikniritið¶

Eftir undirbúning í síðustu tveimur greinum er framsetning k-means reikniritsins afar einföld. Það felst einfaldlega í að reikna aftur og aftur bestu skiptingu fyrir gefna miðpunkta, og endurreikna miðpunktana fyrir skiptinguna sem kom út. Hér er þetta aðeins formlegra:

\[\begin{split}&\textit{k-means:}\\[3pt] &\text{Veljum einhverja miðpunkta }m_1, \ldots, m_k \\ &\textbf{Lykkja}\text{ þar til samleitni náð:} \\ &\qquad \text{Ákvörðum skiptingu með reikniriti }\textit{Besta-skipting}\\ &\qquad \text{Ákvörðum nýja miðpunkta með reikniriti }\textit{Reikna-miðpunkta}\end{split}\]

Það eru ýmsar aðferðir til að velja upphafsgildi miðpunktanna í fyrsta skrefinu. Ein einföld leið er að velja þá af handahófi úr punktasafninu, og önnur er sú að skipta safninu af handahófi í \(k\) hópa og velja upphafsgildi \(m_j\) sem meðaltal \(j\)-ta hóps. Samkvæmt Wikipedíugreininni um k-means þá er aðferð kennd við Bradley og Fayyad betri og sömuleiðis aðferð nefnd k-means++.

Markmiðið með reikniritinu er að reyna að finna skiptingu sem lágmarkar markfallið:

\[d = \sum_{j=1}^k \sum_{i \in G_j} \|x_i - m_j\|^2\]

Hægt er að sýna fram á að markfallið minnkar eða stendur í stað í hverju skrefi, og þar sem það er takmarkað að neðan (verður aldrei minna en 0) og það eru bara endanlega margar flokkanir til þá kemur að því að við tökum skref sem breytir markfallinu ekki. Oftast er ítrekuninni samt hætt fyrr, þegar markfallið breytist um minna en einhver fyrirfram ákveðinn þröskuldur. Þetta gefur nokkurskonar staðbundið lággildi, og stundum er reikniritið framkvæmt nokkrum sinnum með mismunandi byrjunarval á miðpunktunum, og svo valin sú skipting sem endar í besta gildi á markfallinu.

Python:

Í Scipy er pakki sem heitir scipy.cluster.vq sem geymir föll til að flokka vigra. Aðalfallið heitir kmeans en auk þess eru hjálparföll, sér í lagi vq og whiten. Scipy skjölunin kallar vigrana sem flokkaðir eru observations (a.m.k. stundum) og stökin í þeim features. Vörpun frá miðpunktum yfir í hópa er kölluð code book sem þýðir upphaflega dulmálslykill. Hún er útfærð með fylki þar sem röð nr. \(i\) er miðpunktur fyrir hóp nr. \(i\). Orðið code er svo notað um hópnúmer. Markfallið er kallað distortion. Eins og sést hér á eftir skilar fallið kmeans bara miðpunktum fyrir flokkunargögn og svo þarf að kalla á vq til að finna hópnúmer hvers og eins. Hér er dæmigerð notkun þessara falla:

from scipy.cluster.vq import kmeans, vq
X = ...                  # búa til gögn / lesa úr skrá
k = 5                    # Fjöldi hópa
(cb, d) = kmeans(X,5)    # Skilar cb = codebook (5 línu fylki með miðpunktum)
                         # og d = lokagildi markfalls
(code, dvec) = vq(X, cb) # code[i] = hópnúmer vigurs í i-tu línu X,
                         # dvec[i] = fjarlægð hans frá sínum miðpunkti

Athugasemd: Um skömmtun

Vq stendur fyrir vector quantization, en bein þýðing væri vigurskömmtun. Skömmtun (quantization) er hugtak í eðlisfræði sem snýst t.d. um að orka rafeindar í vetnisatómi getur bara tekið tiltekin strjál (discrete) gildi. Sama hugtak er svo notað í tölvunarfræði, t.d. þegar við fækkum litum í litmynd úr milljónum í 256 eða 16, eða þegar við látum þungamiðju eða miðpunkt hóps koma í stað hópsins alls.

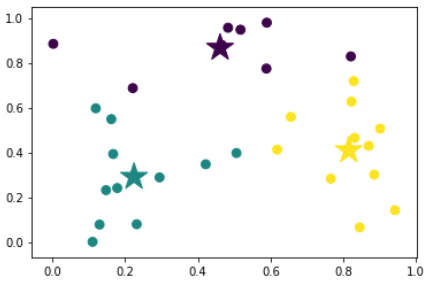
Sýnidæmi: Hópaskipting með forriti

Hér er forrit sem býr til 30 slembipunkta í planinu og skiptir þeim svo í 3 hópa, og prentar út og teiknar niðurstöðuna. Miðpunktar eru teiknaðir með stjörnum.

# UNDIRBÚNINGUR
import numpy as np, numpy.random as npr, matplotlib.pyplot as plt
from scipy.cluster.vq import kmeans, vq
np.set_printoptions(precision=3, floatmode='fixed', suppress=True)
npr.seed(23)
X = npr.rand(30,2)

# FLOKKUN
(cb,d) = kmeans(X, 3)
(code,dvec) = vq(X, cb)

# ÚTPRENTUN OG TEIKNING
print('codebook =\n', cb)
print(f'markfall = {d:.3f}')
print(f'flokkun = {code}')
(x,y) = X.T
(mx,my) = cb.T  # miðpunktar
plt.scatter(x, y, s=60, c=code);
plt.scatter(mx, my, s=600, c=[0,1,2], marker='*');

Úttak:

codebook =
 [[0.461 0.866]
 [0.224 0.291]
 [0.815 0.409]]
markfall = 0.198
flokkun = [0 2 0 1 2 0 2 0 2 1 2 1 2 1 2 2 1 1 2 1 0 2 1 1 0 2 0 1 0 1]

Python:

Til að fá góða liti á hópa sem teiknaðir eru með scatter er upplagt að nota fallið qcmap úr kafla A4 í Viðauka A.

Æfing

Afritið forritið í sýnidæminu og prófið að keyra það með 5, 10 og 20 hópum með sjálfgefnu litunum.
Breytið nú forritinu þannig að qcmap sé notað til að velja liti og berið saman við fyrri niðurstöðu.

3.7 Dæmi um nokkrar k-means-ítrekanir¶

Til glöggvunar fylgja hér nokkrar myndir af niðurstöðum reikniritanna Besta-skipting (t.v. í hverri mynd; sjá grein 3.5) og Reikna-miðpunkta (t.h. í hverri mynd; sjá grein 3.4) þegar k-means reikniritinu er beitt á dæmið sem sýnt er á Mynd 3.1:. Miðpunktar eru sýndir með ferningum

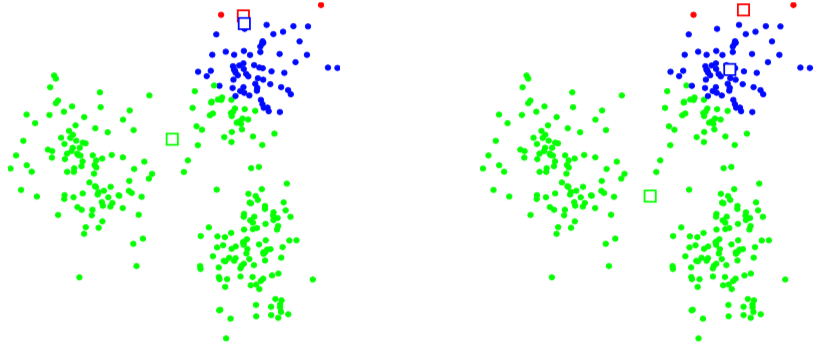
Mynd 3.3: Dæmi um k-means, ítrekun 1¶

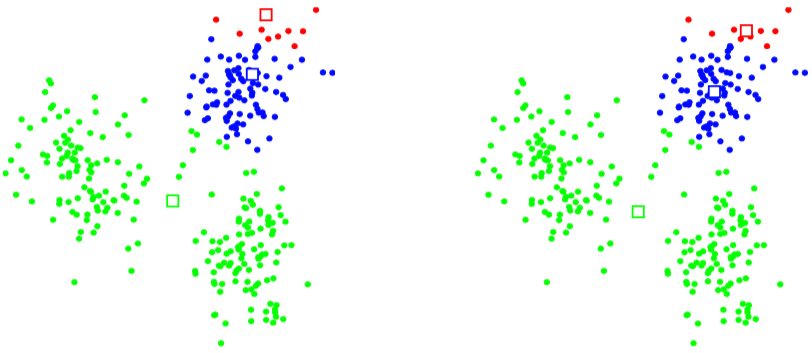
Mynd 3.4: Dæmi um k-means, ítrekun 2¶

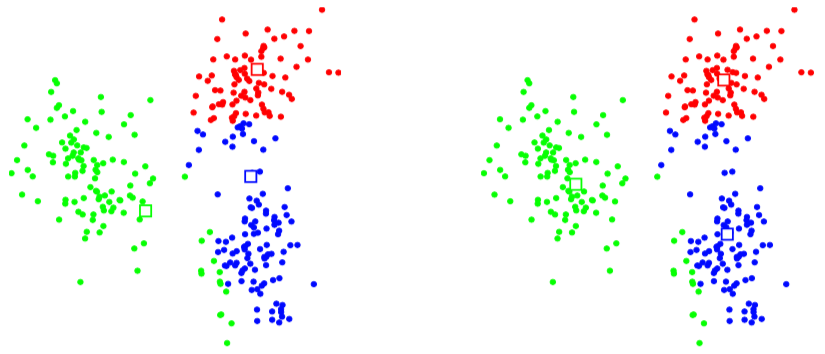
Mynd 3.5: Dæmi um k-means, ítrekun 10¶

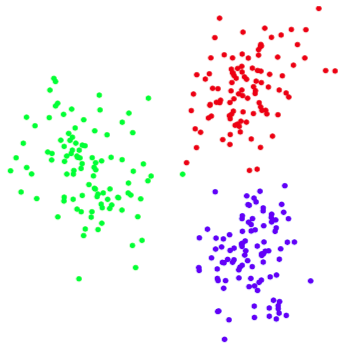
Mynd 3.6: Dæmi um k-means, eftir 15 ítrekanir¶

Lokamyndin er sú sama og er í byrjun kaflans (Mynd 3.1:). Hér er mynd sem sýnir hvernig markfallið (á \(y\)-ás) þróast með númeri ítrekunar (á \(x\)-ás).

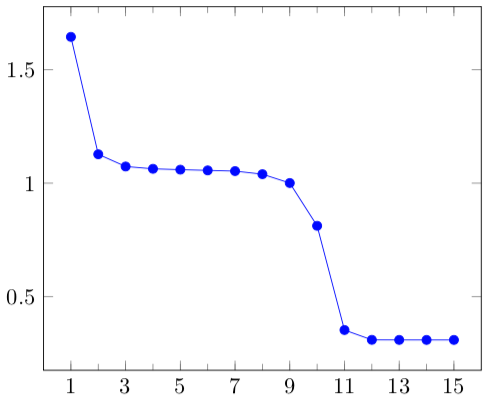
Mynd 3.7: Markfall í k-means sem fall af númeri ítrekunar¶

3.8 Forvinnsla vigra með `whiten`¶

Ef stökin í vigrunum sem á að flokka hafa mjög mismunandi stærðargráðu getur borgað sig að skala þau. Tökum sem dæmi að við ætlum að flokka menn eftir hæð og þyngd, og hæðin sé í metrum en þyngdin í kílóum. Ef ekkert er gert mundu hæðirnar hafa lítil sem engin áhrif á röðun í hópa. Hér væri hægt að staðla hæð og þyngd með því að deila með staðalfrávikum hvors um sig áður en flokkað er.

Python

Eitt af því sem vq-pakkinn býður upp á er fallið whiten sem staðlar hvert einkenni (hnit) með því að deila með staðalfráviki þess, svo öll einkennin hafi staðalfrávik 1. Þannig mætti byrja forritsbútinn í síðustu grein á:

from scipy.cluster.vq import kmeans, vq, whiten
X = ...                  # búa til gögn / lesa úr skrá
X = whiten(X)            # staðla gögn
...

Athugið

Annar vinsæll Python-pakki sem m.a. getur flokkað er Scikit-learn (fluttur inn með import sklearn.cluster o.fl.). Þar er m.a. að finna mjög vinsælan flokkara sem heitir DBSCAN. Hér er áhgugaverð vefsíða með flokkunarmyndum sem búnar eru til með ýmsum flokkurum úr Scikit-learn.