1 Verkefni: Annars stigs jafna¶

Skrifið forrit sem leysir annars stigs jöfnu

\[a x^2 + b x + c = 0\]

Forritið á að lesa inn \(a\), \(b\) og \(c\) með input-skipunum (með viðeigandi beiðnum til notanda). Ef jafnan hefur tvær lausnir á forritið að skrifa „Lausnirnar eru:“ og síðan lausnirnar, ef hún hefur eina lausn á að skrifa hana með viðeigandi skýringu og ef engin lausn er skal skrifa skilaboð um það. Lausn eða lausnir eru gefnar með formúlunni

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

Ef stærðin undir kvaðratrótinni er neikvæð þá er engin lausn, ef hún er núll er ein lausn, annars tvær. Gerið auk þess ráð fyrir þeim möguleika að \(a\) sé 0. Ef \(b\) er ekki líka 0 þá er jafnan fyrsta stigs og forritið á að skrifa að svo sé, ásamt lausninni (sem er þá ein). Látið \(b\) og \(c\) vera gefin með afmælisdegi ykkar (dagur og mánuður) og prófið forritið fyrir fjórar mismunandi jöfnur, fyrsta stigs jöfnuna \(bx + c = 0\) og annars stigs jöfnur sem hafa enga, eina og tvær lausnir þar á meðal jöfnuna \(x^2 + bx + c = 0\). Setjið viðeigandi skjölunarstreng fremst í forritið.

2 Töluleg heildun¶

A. Samsett trapisuregla

Í sýnidæmi og æfingu í kafla 4.9 voru búin til föll til að nálga heildi með flatarmáli einnar eða tveggja trapisa. Föllin voru prófuð með heildunum:

\[(*)\hspace{1cm}\int_1^2\frac{\sin(x)}{x} dx\hspace{1cm}\text{og}\hspace{1cm} (**)\hspace{1cm}\int_0^1 e^x dx\]

og fengust eftirfarandi nálganir:

(*)

(**)

1 trapisa

0.648

1.859

2 trapisur

0.657

1.754

rétt gildi

0.6593299

1.7182818

Enn betri nálgun fæst með samsettri trapisureglu sem notar \(n\) trapisur. Forritið hana og prófið með (*) og (**) og \(n = 4\). Kannið líka hve stórt \(n\) þarf að vera til að fá (næstum) 7 rétta aukastafi, sbr. uppgefin rétt gildi. Hér eru formúlurnar sem þarf að nota ásamt skýringarmynd:

Bilinu \([a,b]\) er skipt upp í \(n\) hlutbil sem hvert hefur lengd \(\Delta x = \dfrac{b-a}{n}\).
Skiptipunktarnir eru: \(a = x_0 < x_1 < x_2 < \cdots < x_n = b\) þar sem \(x_i = a + i\Delta x\).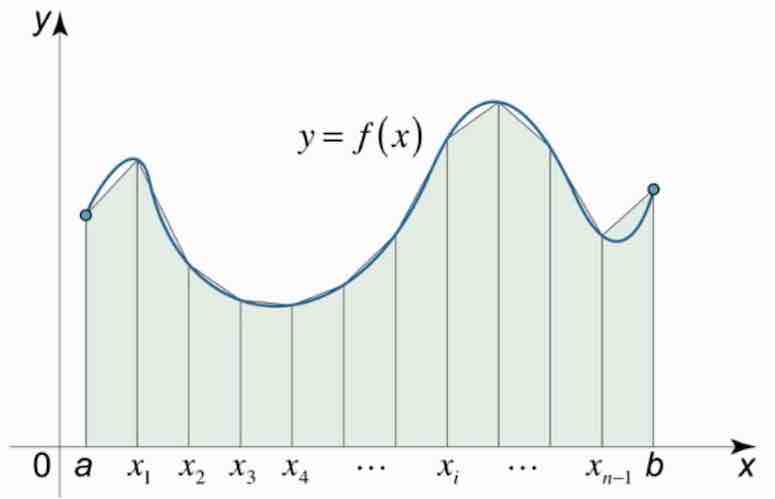

þá fæst nálgunin:

\[\int_{a}^{b} f(x)\,dx \approx T_n = \frac{\Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + \cdots + 2f(x_{n-1}) + f(x_n) )\]

B. Simpsons-regla

Skrifa skal forrit til að nálga heildi með svonefndri Simpsons-regla. Í trapisureglu er heildisbilinu skipt í \(n\) hlutbil, fallið sem heilda skal nálgað með beinum línustrikum og heildi þess nálgað með flatarmálinu undir þessum línustrikum. Í Simpsonsreglu er fallið hinsvegar nálgað (eða brúað eins og það er kallað) með parabólum og heildið nálgað með flatarmálinu undir þeim. Skoðið endilega Wikipedíu-grein um aðferðina.

Simpsons-formúlan er eftirfarandi:

\[\int_{a}^{b} f(x) \, dx \approx \frac{\Delta x}{3}\left(f(x_0) + 4f(x_1)+2f(x_2)+ 4f(x_3)+2f(x_4)+\cdots+4f(x_{n-1}) + f(x_{n})\right)\]

þar sem \(\Delta x\) og \(x_i\) eru eins og í A-lið og \(n\) er slétt tala.

Skrifið fall simpson(f,a,b,n) sem nálgar heildið af f frá a til b með samsettri Simpsons-reglu með n hlutbilum.

Prófið með heildunum (*) og (**) úr A-lið með 4 hlutbilum. Ef rétt er forritað ætti að fást \((*)\) 0.65933 og \((**)\) 1.71832. Kannið líka hve stórt \(n\) þarf að vera til að fá alla 7 aukastafina sem gefnir eru í töflunni í A-lið rétta. Heildið a‘ lokum eitthvert sjálfvalið fall þar sem afmælisdagur ykkar kemur við sögu.

3 Ýmis dæmi¶

A. Hitastigum breytt

Hitastig í Fahrenheitgáðum er \(T_F = \frac{9}{5}T_C + 32\) þar sem \(T_C\) er hitastigið í Celcíusgráðum. Skrifið forrit sem skrifar út töflu til að breyta milli skalanna sem nær frá \(–30^\text{o}C\) til \(50^\text{o}C\) og hleypur á \(5^\text{o}C\). Á Makka fæst gráðumerki með option-T og á Windows með Alt-0176. Taflan gæti byrjað svona:

°C    °F
–––––––––
-30   -22
-25   -13
-20    -4
-15     5
...

B. Rætur, lograr, kvaðröt

Skrifið forritsbút með for-lykkju sem finnur kvaðratrætur, náttúrulega logra, og önnur veldi talnanna 1–10. Notið F-strengi til að skrifa (fallega) töflu yfir niðurstöðuna. Hafið 2 aukastafi í kvaðratrótunum og logrunum.
Endurtakið með while-lykkju.

C. Lograr og veldi

Til að reikna logra (lógaritma) hefur Python þrjú föll: Náttúrulegur logri fæst með log(x), tíu-logri fæst með log10(x) og loks fæst logri með grunntölu 2 með log2(x). Fastinn \(e\) fæst með math.e, og vísisfallið, \(e^x\), fæst með exp(x). Reiknið:

\(\ln(1)\)
\(\ln \exp(3)\)
\(\log_{10} 1000\)
\(\log_2 8\)

(Ætti að gefa 0, 3, 3 og 3)

D. Rúmmál kúlu

Þetta dæmi og það næsta (taflborðið) eru æfingar í útprentun, en ekki síður æfingar í að byggja upp forrit úr minni einingum, sem maður prófar hverja fyrir sig og setur svo saman.

Skrifið Python fall sem reiknar og skilar rúmmáli kúlu með radíus r. Prófið með kúlu með radíus 2 (ætti að skila 33.51)
Skrifið fall sem reiknar og skilar radíus hrings með gefið ummál. Prófið.
Skrifið fall sem tekur inn eðlismassa hlutar í \(\text{g/cm}^3\) og rúmmáli hans í \(\text{m}^3\) og skilar þyngd hans í kg. Notið fallið til að reikna þyngd gulltenings sem er 20 cm á kant (eðlismassi gulls er 19.30; ætti að skila 154.4 kg).
Jörðin er um það bil kúla með ummál 40 þúsund km og eðlisþyngd hennar er 5.5 \(\text{g/cm}^3\). Notið föllin í liðum 1–3 til að finna massa jarðar í tonnum.

Látið öll forritin skrifa stuttan skýringartexta með því sem er prentað.

E. Taflborð

Lokamarkmiðið þessa dæmis er að búa til fall sem prentar út \(n \times n\) taflborð fyrir slétta tölu \(n\) sem lítur svona út þegar \(n=8\):

+-----------------+
|   X   X   X   X |
| X   X   X   X   |
|   X   X   X   X |
| X   X   X   X   |
|   X   X   X   X |
| X   X   X   X   |
|   X   X   X   X |
| X   X   X   X   |
+-----------------+

Það eru þrjár gerðir af línum:

Efsta og neðsta línan, með \(+\), \(2n + 1\) striki og aftur \(+\).
Línur eins og önnur línan með þrjú bil og X endurtekið \(n/2\) sinnum.
Línur eins og þriðja línan með X og þrjú bil endurtekið \(n/2\) sinnum

Skrifið þrjú föll, til að prenta línur af tagi a, b og c. Prófið hvert um sig fyrir \(n=2\) og \(n=8\).
Skrifið fall sem kallar á föllin í lið 1. og prentar \(n \times n\) borð. Látið fallið skrifa villuboð og hætta ef \(n\) er ekki slétt tala > 2. Prófið með \(n=8\)

Munið að nota *-virkjann, sem fjölfaldar strengi.

F. Viðsnúningur lista

Skrifið fall hali(L) sem skilar hala L, þ.e. lista með öllum stökum nema því fremsta.
Skrifið fall hausaftast(L) sem skilar nýjum lista þar sem haus L hefur verið færður aftast. Ef kallað er með L=[1,2,3,4] ætti fallið að skila [2,3,4,1]. Prófið líka með lista búnum til útfrá afmælisdegi (t.d. 3.8.1999 \(\to\) [3,8,99]).

Skrifið fall snúavið(L) sem snýr við lista. Hér er reiknirit:

fall snúavið(L)
    n := lengd L
    M := tómur listi
    fyrir i = n-1,n-2,...,0:
        setja i-ta stak L afast í M
    skila M

Prófið að snúa við L=[1,2,3,4] sem ætti að skila [4,3,2,1] og líka afmælisdagalistanum úr lið 2.

4 Orðaleikur¶

Skrifið fall telja(s) sem byrjar á nota s.split() til að búa til lista af einstökum orðum í s og telur síðan hve margir stafir eru í hverju orði. Fallið á að skila lista með þessari talningu. Þannig ætti

telja("Afi minn og amma mín")

að skila listanum [3,4,2,4,3]. Prófið líka að telja stafi í nafninu ykkar (t.d. telja("Kristján Jónasson")). Líklega borgar sig að búa fyrst til tóman lista og fara svo í lykkju og bæta nýrri talningu afast í listann í hverri umferð (t.d. með append).
Búið til fall hrópa(s) sem skrifar s út með stórum stöfum og tveimur upphrópunarmerkjum. Hrópið svo nafnið ykkar :)
Til að athuga hvort stafur c sé hástafur má spyrja: c == c.upper(). Skrifið fall stórir(s) sem skilar lista af rökgildum með i-ta gildið satt ef i-ta orðið í s byrjar á stórum staf. Prófið með sjálfvöldu dæmi og sýnið niðurstöðuna.

5 Kvaðratrót¶

Um útreikning kvaðratrótar er fjallað í kafla 7.5 í Think Python kennslubókinni. Þar stendur að hægt sé að nota Newtons aðferð, og að ef byrjað er með einhverja nálgun \(x\) við \(\sqrt{a}\) þá fáist betri nálgun, \(y\) með því að reikna:

\[(*)\hspace{4cm} y = \frac{x + a/x}{2}\]

Formúluna má m.a. rökstyðja þannig að ef \(x\) er nákvæmt gildi þá er \(x^2 = a\) svo að \(x = a/x\). Hinsvegar ef \(x\) er aðeins minna en kvaðratrótin þá þá verður \(a/x\) aðeins stærra en hún (og öfugt) og því ætti meðaltal \(x\) og \(a/x\) að vera betri nálgun. Svo má athuga hve nálgunin er góð með því að skoða muninn á \(x\) og \(y\). Ef t.d.

\[(**)\hspace{4cm}|x - y| < \varepsilon\]

þar sem \(\varepsilon = 10^{-4}\) er hún orðin nokkuð góð.

Skrifið Python-fall, krót(a) sem útfærir þessa hugmynd. Byrjið með upphafsgildið x = 1 og finnið svo betri og betri lausn með því að nota while-lykkju sem reiknar \((*)\) aftur og aftur og heldur áfram þangað til \((**)\) er uppfyllt. Prófið að reikna \(\sqrt{9}\) og \(\sqrt{10}\) (rétt gildi 3.16227766017).
Búið nú til nýja útgáfu af fallinu sem er með tvo inntaksstika, töluna a og nákvæmnikröfu eps, og telur auk þess hve margar ítrekanir eru teknar. Látið það skila bæði lokanálguninni og ítrekanafjöldanum (sbr. fyrra sýnidæmið í kafla 4.7). Skrifið niðurstöður með hæfilegum skýringartextum: lokanálgun, ítrekanafjölda, og muninn á réttri kvaðratrót og lokanálgun. Prófið með nokkrum mismunandi gildum á \(a\) (m.a. eitthvað mjög stórt gildi) og \(\varepsilon\), (m.a. gildi sem er ekkert mjög lítið, t.d. 0.1 eða 0.01). Bætið við textareit og skrifið örfá orð um niðurstöðu þessarar prófunar.

6 Meðaltal og staðalfrávik¶

Skrifið fall tölfræði(x) sem skilar pari (m, s) með meðaltali og staðalfráviki stakanna í listanum x með því að nota formúlurnar:

\[\begin{split}m &= \frac{1}{n}\sum_{i=0}^{n-1}{x[i]}\\ s &= \sqrt{\frac{1}{n-1}\sum_{i=0}^{n-1}(x[i] - m)^2}\end{split}\]

Prófið með x = [3,7,7,1] (á að skila [4.5, 3.0]) og líka með lista [d,m,á] búnum til úr fæðingardegi.

7 Bóluröðun¶

Hér er reiknirit sem raðar n-staka lista x með bóluröðun bubble sort, sem snýst um að rúlla í gegn um stökin og ef tvö samliggjandi stök eru í öfugri röð þá er víxlað á þeim. Þetta er endurtekið þar til öll stökin eru í röð. Minnstu stökin bobbla smám saman eins og loftbólur fremst í listann.

víxlað = satt
meðan víxlað
   víxlað = ósatt
   fyrir i=1,...,n-1:
      ef x[i-1] > x[i] þá
         víxla á x[i-1] og x[i]
         víxlað = satt

Þýðið þetta reiknirit yfir í Python-fall bóluröðun(x). Athugið að til að víxla á breytum x og y má nota (x,y) = (y,x). Prófið með því að raða listanum [3,8,1,2,5,4].

8 Pólhnit¶

Lesið aðeins um pólhnit á Wikipediu áður en þið spreytið ykkur á eftirfarandi verkefni.

Skrifið fall pol2rec(r,theta) sem skilar pari (x,y), til að breyta úr pólhnitum yfir í rétthyrnd hnit með eftirfarandi formúlum:

\[\begin{split}x &= r \cos{\theta}\\ y &= r \sin{\theta}\end{split}\]

Prófið að breyta \((r,\theta) = (4,35°)\) yfir í rétthyrnd hnit \(x\) og \(y\) (á að gefa \(x=3.277\), \(y=2.294\)). Munið að nota math.radians til að breyta gráðum í radíana.
Skrifið svo annað fall, rec2pol(x,y) sem skilar (r,theta) og breytir í hina áttina með formúlunum:

\[\begin{split}\theta &= \operatorname{atan2}(y,x)\\ r &= \sqrt{x^2 + y^2}\end{split}\]

Prófið að breyta svarinu sem fékkst í lið 1 aftur til baka í pólhnit.

Athugasemd

Stærðfræðifallið atan2 sem er líka til í Python er sérhannað til að breyta úr rétthyrndum hnitum í pólhnit. Það skilar horni \(\theta\) á bilinu \((-\pi,\pi]\) þannig að \(\tan \theta = y/x\), nema ef \(x=0\), þá skilar fallið \(\pm\pi/2\) með sama formerki og \(y\). Hornið er valið þannig að það sé stefnuhorn vigursins \((x,y)\).

9 Innsetningarröðun og Pythontutor¶

Ein einfaldasta röðunaraðferðin er innsetningarröðun (insertion sort). Forritið fyrsta reikniritið í lýsingu hennar á Wikipediu í Python falli. Notið paragildisgjöf, (x,y) = (y,x) til að víxla (swap) í 5. línu reikniritsins. Prófið að raða listanum [3,8,1,2,5,4]. Leysið verkefnið með falli sem hefur listann sem raða skal sem inntaksstika og skilar röðuðum lista. Gætið þess að breyta ekki inntaksstikanum inni í fallinu.
Á vefsíðan pythontutor.com er hægt að keyra forrit skref fyrir skref og skoða hvernig gildi á breytum breytast. Setjið forritið sem þið skrifuðuð í lið 1 inn á þessa síðu og prófið ykkur áfram.

10 Töluleg diffrun¶

Eftirfarandi formúlu má nota til að nálga afleiðu falls í punkti \(a\):

\[f'(a) \approx \frac{f(a+h) - f(a-h)}{2h}\]

þar sem \(h\) er lítil tala. Skrifið fall töldiff(f, a, h) sem reiknar slíka nálgun og skilar henni. Prófið með \(f(x) = \sqrt{x}\), \(a = 4\) og \(h = 10^{-4}\) (sem ætti að skila tölu sem er nálægt \(\frac{1}{2\sqrt{4}}\)).
Skrifið nú töflu yfir nálgunina fyrir \(h = 10^{-k}, k=1,...10,\) og látið fylgja með dálk sem sýnir hve skekkjan er mikil. Merkið með \(*\) línuna þar sem skekkjan er minnst.

11 Uppflettitafla afturábak¶

Hugsum okkur að ísl_ens sé uppflettitafla sem geymir íslensk-enska orðabók. Hún gæti t.d. innihaldið pörin:

"reipi" \(\to\) "rope"
"hús" \(\to\) "house" og
"rauður" \(\to\) "red".

Ef við vilum búa til ensk-íslenska orðabók gætum við snúið töflunni við og fengið pörin "rope" \(\to\) "reipi", "house" \(\to\) "hús" o.s.frv.

Skrifið fall snúavið(U) sem snýr uppflettitöflu við á þennan hátt og skilar viðsnúnu töflunni. Gerið ráð fyrir að taflan U hafi hvergi sama gildi fyrir tvo mismunandi lykla. Prófið með orðaskránni að framan og búið til ens_ísl.
Skrifið nýja útgáfu af fallinu, snúavið2(U), sem er ekki með slíkri einkvæmnitakmörkun. Það á að skila nýrri uppflettitöflu V sem er þannig að ef g er gildi svarandi til tveggja mismunandi lykla, U[x] = U[y] = g þá á gildi V fyrir lykilinn g að vera listi með x og y, V[g] = [x,y]. Bætið nú tveimur pörum við ísl_ens:

"tómarúm" \(\to\) "vaccum"
"ryksuga" \(\to\) "vaccum"

og prófið snúavið2.

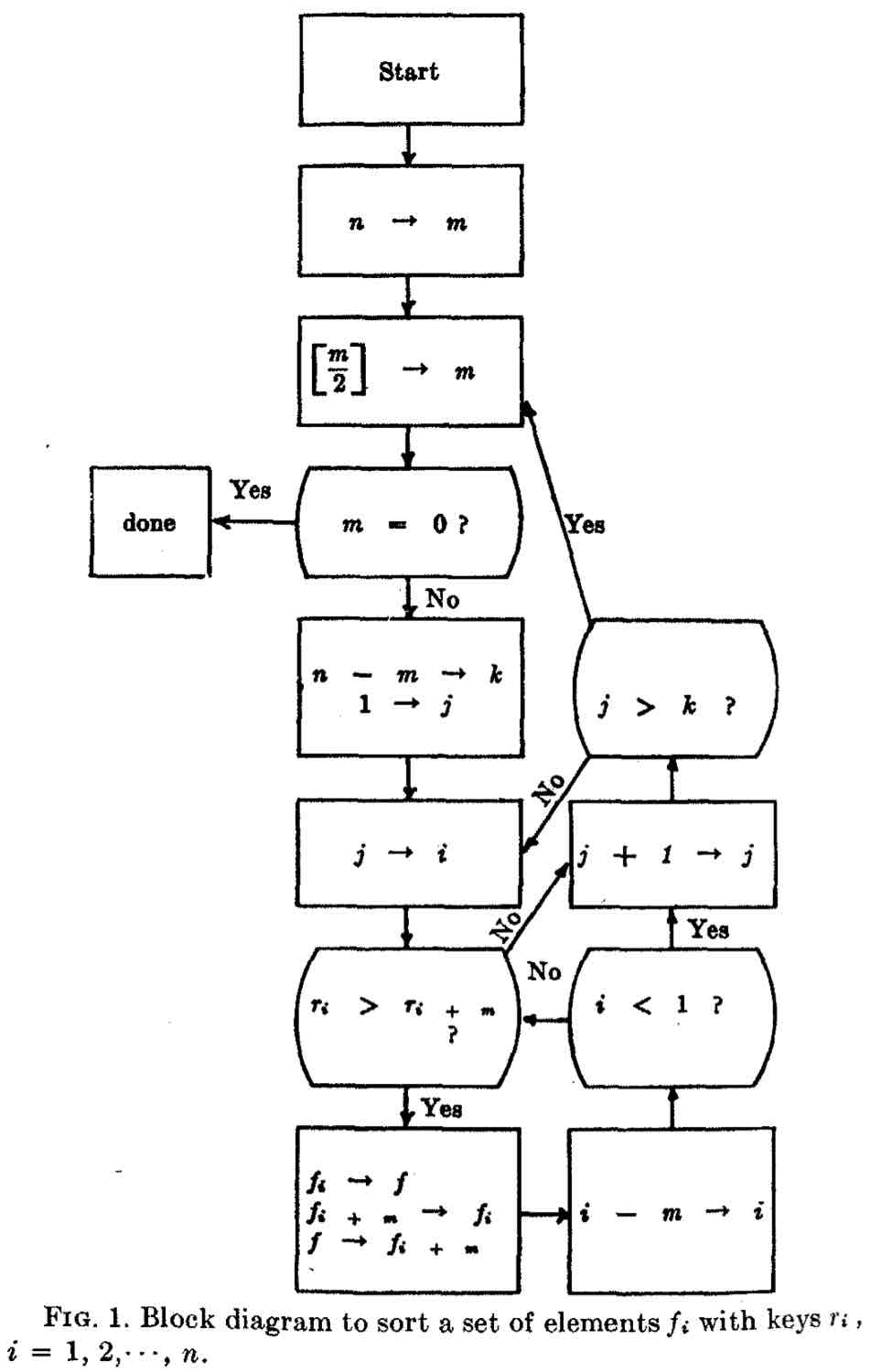
12 Shell-röðun¶

Árið 1959 kom út grein eftir Donald L Shell með hraðvirku reikniriti til að raða \(N\) tölum (eða öðrum hlutum) sem síðar var kallað Shell-sort. Það er áhugavert að skoða greinina, sérstaklega hvernig reikniritið er sett fram með svonefndu flæðiriti, en í byrjun tölvualdar voru þau algeng. Reikniritið vinnur með minnkandi runu af bilum (gaps), \(b_1 > b_2 >...> b_n = 1\). Í fyrstu umferð er sætum \(0, b_1, 2b_1,\ldots\) raðað með innsetningarröðun (sjá verkefni 9), þvínæst sætum \(1, 1+b_1, 1+2b_1,\ldots\), o.s.frv. þar til allar hlutrunur sæta með millibili \(b_1\) eru komnar í röð. Þetta er svo endurtekið fyrir öll bilin. Í upphaflegu grein Shells var \(b_k\) valið sem \(\left\lfloor N/2^k \right\rfloor\) en síðan hafa menn þróað ýmsar aðrar bilarunur (\(\left\lfloor x \right\rfloor = \operatorname{int}(x)\); þ.e. sker aukastafi af \(x\)).

Hér er reiknirit sem Shell-raðar lista a[0],a[1]...a[N-1] með upphaflegu bilarununni:

fyrir k = 1,2,3,...:
   bil = int(N/2^k)
   ef bil < 1 þá út úr lykkju
   fyrir i = 0, 1,..., bil-1:
       raða a[i], a[i+bil], a[i+2*bil],... með innsetningarröðun

Skrifið Python-fall sem Shell-raðar. Byrjið á að leysa verkefni 9 ef þið eruð ekki þegar búin að því. Það er hægt að nota heiltöludeilingu (//) til að reikna bil og hlutrunan í neðstu línunni fæst með a[i:N:bil]. Byggið á reikniritinu að framan (og alls ekki ná í tilbúið forrit af netinu). Prófið að raða listunum [8,3,2] og [8,5,1,9,6,2,1,7,11,3], og auk þess einum sjálfvöldum lista með 12 tveggja stafa tölum.

13 Skrá með íslenskum orðum¶

Þetta verkefni er lauslega byggt á verkefnum í 9. kafla Think Python kennslubókarinnar. Í skrá með veffang https://cs.hi.is/python/ord.txt eru 217 þúsund íslensk orð. Þið getið skoðað skrána með því að smella á hlekkinn. Í verkefninu sem hér fylgir þarf að nota ýmsar strengjaaðgerðir sem lýst er í kafla 5.2.

Opnið skrána með urlopen og lesið hana inn eins og sýnt er í kafla 8.2.4. Prentið út fyrstu 5 orðin og líka tíu þúsundasta hvert orð og öll orð sem eru lengri en 30 stafir.

Leiðbeining

Það er bara eitt orð á hverri línu sem hægt er að ná í með orð = lína.decode().strip()

Athugasemd

Í stað þess að nota urllib mætti lesa skrána inn með NumPy eins og fjallað er um í kafla 10.7.2. Þá er notað dtype=str í sjálfum innlestrinum, og síðan má nota tolist-aðferðina til að breyta innlesnum vigri í venjulegan lista af strengjum.
Spegilorð (palindrome) er orð sem er eins lesið afturábak og áfram (t.d. kajak). Skrifið rökfall spegilorð(s) sem kannar hvort s sé spegilorð [rökfall er fall sem skilar True eða False og prófið. Skrifið í framhaldi út öll spegilorð í skránni, 10 á hverja línu. Fyrsta linan ætti að verða:

abba, afa, aga, agga, aka, ala, alla, ama, amma, ana,

Leiðbeining

Til að snúa við streng s má nota s[::-1]. Það þarf að nota end= í print-skipun sbr. kafla 4.4, og svo þarf að nota teljara sem fylgist með hvað er búið að prenta mörg orð á línuna og þegar þau eru orðin 10 er farið í nýja línu með print() og teljarinn núllstilltur. Fyrsta línan sem prentast ætti að vera:
Finnið þau orð í skránni sem hafa einn sérhljóða og hámarksfjölda samhljóða.

Athugasemd

UTF-8 er staðall til að geyma bókstafi og önnur rittákn í tölvum. Staðallinn hefur á síðasta áratug eða svo orðið alsráðandi í tölvuheiminum, og eru 97% allra vefsíðna skráð með honum. Hver stafur er geymdur í einu til fjórum bætum. Algengustu tákn og stafir, þ.m.t. allir enskir bókstafir nota eitt bæti, aðrir bókstafir allra evrópskra tungumála þurfa tvö bæti, en sjaldgæfari stafir og tákn þurfa þrjú eða fjögur bæti. Strengir í forritunarmálum, þ.m.t. Python eru hinsvegar ekki geymdir með UTF-8 sniði heldur ýmist sem Latin-1, UTF-16 eða UTF-32. Þetta er gert til að öll tákn hvers strengs séu jafn mörg bæti, sem flýtir t.d. fyrir uppflettingu á i-ta sæti.

14 Fjöldi stafa í skrafli¶

Í þessu verkefni á að búa til töflu yfir hlutfallslega tíðni hvers stafs í skránni ord.txt úr verkefni 13, og jafnframt hvað sú tíðni samsvarar mörgum heilum stöfum af 98, sem er heildarfjöldi stafa í pokanum sem notaður er í borðspilinu skrafli (scrabble). Taflan ætti að byrja svona:
```
stafur  tíðni  fjöldi
–––––––––––––––––––––
  a     9.80%    10
  á     1.27%     1
  b     1.34%     1
```
Leiðbeiningar

Byrjið á að skoða athugasemdina að neðan, þ.m.t. vefsíðu netskraflara. Skrána ord.txt má opna og lesa inn annaðhvort með urllib eða NumPy, eins og í verkefni 13 . Ef s er strengur og L er listi af strengjum þá má skeyta þeim saman aðskildum með s með því að rita s.join(L), til dæmis:
```
L = ["már", "mús", "mý"]
s1 = ",".join(L)         # gefur "már,mús,mý
s2 = "".join(L)          # gefur "mármúsmý"
```
Þannig má fá langan streng öllorð með öllum orðum skrárinnar í runu með því beita join með tóma strengnum á útkomuna úr allarlínur. Skoðið byrjunina á öllorð með print(öllorð[:40]). Svo má t.d. finna hlutfallslega tíðni a með ta = öllorð.count("a")/n þar sem n = len(öllorð). Tilsvarandi heill fjöldi a-a af 98 fengist með round(ta*98). Hægt er að rúlla í gegn um alla stafina með for-lykkju og strengnum:

stafróf = "aábcdðeéfghiíjklmnoópqrstuúvwxyýzþæö"
Aukaspurning: Ef rétt er reiknað sést að allmargir stafir gefa fjöldann 0. Í skrafli er hinsvegar amk. einn stafur af hverri gerð í pokanum. Ef við hækkum öll núllin upp í einn fást of margir stafir. Lýsum einni leið til að leiðrétta það. Byrjum á að búa til uppflettitöflu fj þannig að fj[c] sé fjöldi af staf c skv. lið 1, nema við látum fj[c] = max(1,round(ta*98)). Hér er tilvalið að nota yfirgrip. Við látum:
```
búnir = [c for c in stafróf if fj[c] == 1]
eftir = [c for c in stafróf if fj[c] > 1]
N = 98 - len(búnir)
```
Nú má fara aftur í gegn um lykkju eins og í lið 1, nema hvað aðeins er rúllað í gegn um stafina í eftir, í stað 98 kemur N, og svo þarf n að vera fjöldi stafa í skránni sem eru í eftir. Aftur er hægt að nota yfirgrip:

n = sum([öllorð.count(c) for c in eftir]).

Útfærið þessa hugmynd og athugið hver heildarfjöldi stafa verður.

Athugasemd: Um skrafl

Í skrafli eru mismargir stafir af hverri gerð í pokanum eins og skoða má á vefsíðu netskraflara: það eru t.d. ellefu a, og átta r, en ekki nema tvö ó og eitt h. Stafirnar gefa líka mismunandi mörg stig. Fjöldi eintaka af hverjum staf er nokkurnveginn í hlutfalli við tíðni stafanna í íslenskum orðalista svipuðum þeim sem er í skránni ord.txt, og gildi hvers stafs er líka tengt þessari tíðni.

15 Sameining nafnaskrár og einkunnaskrár¶

Útbúnar hafa verið tvær skrár með gervigögnum: Sú fyrri, https://cs.hi.is/python/einkunn.txt inniheldur prófnúmer og einkunnir og sú seinni, https://cs.hi.is/python/nofn.txt, inniheldur prófnúmer og nöfn.

Skrá lesin. Skrifið forrit sem les einkunnaskrána inn í uppflettitöflu (dictionary) eink_tafla þannig að eink_tafla[nr] gefi einkunn próftaka með prófnúmer nr sbr. dæmin í kafla 8.2.5. Prófið (t.d. með því að sýna úttakið sem skipunin print(eink_tafla) skilar).
Uppflettitafla. Skráin nofn.txt byrjar svona:
```
0176  Kjartan Valur Jónsson
0542  Aðalheiður Pétursdóttir
0970  Sigrún Ása Jónsdóttir
```
Prófnúmerið er sem sé aðskilið frá nafninu með tveimur bilum og svo er nafnið ýmist með millinafni eða án. Til að höndla þetta er hægt að nota split með viðbótarviðfangi sem tilgreinir hve oft á að skipta. Ef lína er fyrsta línan í skránni mundi

(nr,nafn) = lína.decode().strip().split(maxsplit=1)

skipta strengnum rétt í tvo hluta, númer og nafn (strip() þarf að vera með hér til að losna við línuskiptatákn). Notið þetta trix til að lesa nafnaskrána inn í uppflettitöflu nafn_tafla sem nota má til að fletta upp á nafni útfrá prófnúmeri. Prófið með sama hætti og fyrr.
Útskrift lista. Skrifið forrit sem rennir í gegn um prófnúmerin í eink_tafla, flettir upp nafni hvers nemanda í nafn_tafla, og skrifar allt þrennt: prófnúmer, einkunn, og nafn í snyrtilegri töflu með fyrirsögnum og dálkum sem standast á.
Hæsta einkunn. Skrifið loks forrit sem ákvarðar hver fékk hæstu einkunnina og skrifar nafn hans/hennar ásamt einkunninni (gera má ráð fyrir að það sé bara einn). Notið lykkju og uppfærið inni í lykkjunni, í hvert sinn sem einkunn er hærri en sú hæsta sem sést hefur, bæði hæstu einkunnina og nafn þess sem hana fékk. Forritið ætti að skrifa: Íris María Birgisdóttir var hæst með 10.0).

Athugasemd: Lausn með NumPy

Forritin í liðum 1 og 2 má líka útfæra með NumPy; liður 1 er einfaldur: dálkar skrárinnar eru lesnir inn með np.loadtxt (sbr. kafla 10.7) og svo er uppflettitaflan búin til með dict(zip(...)), eins og í seinna sýnidæminu í 8.2.5. Aftur er nafnaskráin erfiðari. Einn möguleiki er að lesa hana inn með L = np.loadtxt(..., dtype=str, delimiter=','). Af því að það eru engar kommur í skránni skilar þetta lista með línum skrárinnar. Svo mætti ná í númerin með yfirgripi (comprehension) svona:

nr = [l.split(maxsplit=1)[0] for l in L]

og nöfnin með samskonar hætti þar sem [1] kemur í stað [0]

Athugasemd: Lausn með Pandas

Það er líka hægt nota Pandas í liðum 1 og 2. Skrárnar má lesa með pd.read_fwf (sjá töflu 15.3). Með því falli leysist flækjan í innlestrinum í lið 2 eiginlega sjálfkrafa því Pandas skoðar skrána og finnur sjálfkrafa út hvernig á að skipta hverri línu í númer og nafn. Athugið að nota þarf bæði names=... og dtype=str. Svo er hægt að nota dict(zip(...)) eins og með NumPy, og zippinu má beita beint á Pandas-dálkana eins og nefnt er í kafla 15.4.

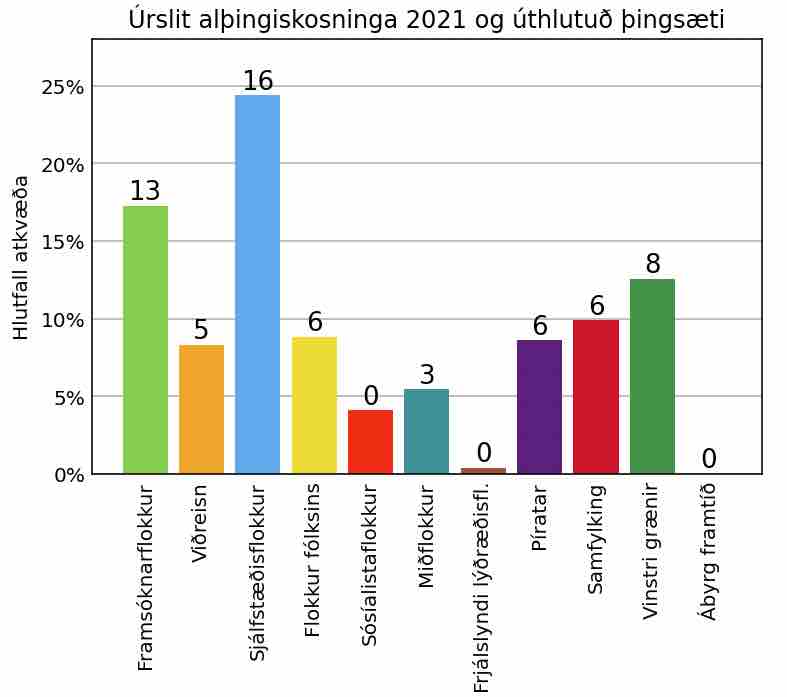
16 Kosningaúrslit¶

Útprentun úrslita. Í skránni https://cs.hi.is/python/kosningar-2021.txt eru úrslit nýjustu Alþingiskosninga (eftir endurtalningu í NV-kjördæmi). Lesið skrána, annaðhvort með hjálp urlopen (sbr. kafla 8.2.4 og 9.3.2) eða með NumPy, og skrifið niðurstöðuna með eftirfarandi sniði:
```
Flokkur Atkvæði Hlutfall Þingsæti
–––––––––––––––––––––––––––––––––
   B     34501    17.3%     13
   C     16628     8.3%      5
...
```
Athugið að það þarf að lesa alla töfluna inn í lista fyrst svo hægt sé að reikna heildarfjölda atkvæða til að geta reiknað hlutfall hvers flokks.
Aukamenn. Það eru nokkuð flóknar reglur notaðar til að finna þingsætafjöldan og ekki víst að alltaf komi sanngjörn niðurstaða. Til að skoða það mætti reikna svonefnda sætishluti, eða þingsætin sem brot, og sleppa þeim flokkum sem ekki komu manni inn (til þess þarf að fá 5% heildaratkvæða, og J, O og Y náðu því ekki). Það eru alls 63 þingsæti, og ef \(A\) er heildaratkvæðafjöldi þeirra flokka sem komu inn manni og \(a_i\) eru atkvæði flokks \(i\) þá er sætishlutur hans

\[s_i = 63 \frac{a_i}{A}\]

Búið til forrit til að skrifa út töflu eins og í lið 1, en bara með þeim 8 flokkum sem komu manni að, og með viðbótardálki með sætishlutunum.

Bætið svo við textareit og segið örfá orð um það hvort niðurstaðan hafi verið sanngjörn eða hvort einhver flokkur (eða flokkar) hafi grætt (fengið aukamann), og þá á kostnað hverra.
Tafla með flokkanöfnum. Í skránni https://cs.hi.is/python/flokksnofn.txt eru listabókstafir í fyrsta dálki og þar fyrir aftan eru nöfn flokkanna, sem geta verið tvö eða fleiri orð. Lesið þessa töflu inn í uppflettitöflu eins og gert er í verkefni 15b. Reyndar er skráin með tab-táknum á eftir listabókstöfumum sem auðveldar aðeins NumPy innlestur, því hægt er að tilgreina delimiter = "\t" til að aðgreina listabókstafi og flokksnöfn, t.d.

(bókst, flokkur) = np.loadtxt(url, delimiter='\t', dtype=str).T.tolist()

Skrifið svo út töflu eins og gert var í lið 1, en með nýjum dálki með nöfnum flokkanna, sem flett er upp í uppflettitöflunni.

Athugið að allar töflurnar sem þið prentið út þurfa að vera snyrtilegar, með fyrirsögnum, hæfilegum aukastafafjölda í tölum, vinstri-jöfnuðum textadálkum og hægri-jöfnuðum talnadálkum.

17 Dálkar í CSV-skrá [leyst með Colab]¶

Í kafla 8.3.6 var skoðað hvernig hægt er að lesa dálk úr CSV-skrá og hér æfum við okkur í því, og líka hvernig búa má til skrár.

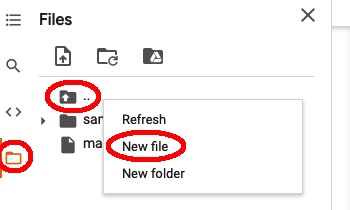
Ný textaskrá í Colab. Það er hægt að búa til skrá í content möppunni í Colab með því að smella á möppu- táknið á vinstri spássíu, hægri-smella svo á möppuna með upp-örinni og velja svo New file sbr. myndina hér t.h.

Síðan má opna skrána með því að tvísmella á hana og svo má slá gögn inn í hana. Með því að smella á nafn skrárinnar efst í hægri spássíu vistast breytingar. Notið þessa aðferð til að búa til skrá malmar.txt með innihaldinu sem er sýnt í kafla 8.3.4 (og líka hér).
Náð í dálk. Hér á að ná í lista með eðlisþyngdum. Búið til lesara fyrir málma-skrána eins og gert er í kafla 8.3.4, en breytið honum svo í lista í staðinn fyrir að nota hann í for-lykkju, eins og útskýrt er í kafla 8.3.6. Náið loks í eðlisþyngdirnar úr dálki 1 sem kommutölur eins og líka er útskýrt í þeim kafla.
Skrá hlaðið niður og upp. Prófið að lokum að hlaða skránni niður frá Colab-skýinu, breyta henni með ritli á eigin tölvu og hlaða henni aftur upp.

18 Fallateikning¶

Skrifið forrit sem reiknar fallsgildi fallsins:

\[f(x) = (x+3)(x+2)x(x-2)(x-3)\]

Prófið t.d. að reikna f(1) (á að gefa 24)
Búið til vandaða teikningu af fallinu á bilinu \([-3.4, 3.4]\) sbr. kafla 9.6. Notið linspace fallið og stikana/föllin xlim, ylim, xticks, yticks, linewidth, color, axvline, axhline, grid, box og tick_params með hæfilegum viðföngum.

19 Hiti og úrkoma¶

Í þessu verkefni ráðið þið hvort þið lesið gögnin með aðstoð urlopen (sjá kafla 8.2.4 og 9.3.2), csv-lesara (sjá 8.3.6) eða NumPy (sjá 10.7).

Veðurskrá lesin. Í skránni cs.hi.is/python/hiti-urkoma.txt eru gögn um meðalárshita og úrkomu í Stykkishólmi 1949–2018. Lesið gögnin í skrána inn í þrjá lista og prentið út upplýsingar fyrir fyrstu 5 og síðustu 5 árin (x[-5:] gefur öftustu 5 stök í x).
Meðalhiti og köld ár. Notið föllin í köflum 6.3 og 6.4 til að finna:
- meðalhita allra áranna (summa deilt með fjölda)
- kaldasta árið og meðalhita þess (notið min til að finna hitann og R.index til að finna árið)
- hve mörg ár voru með meðalhita undir 3°C (hér má nota yfirgrip (comprehension) sem býr til lista af rökgildum og svo R.count() en það má líka nota einhverja aðra aðferð).

Línurit af hita. Teiknið línurit af hitanum með ártal á x-ás ásamt 11 ára hlaupandi þríhyrningsmeðaltali sem lítur svona út eða því sem næst:

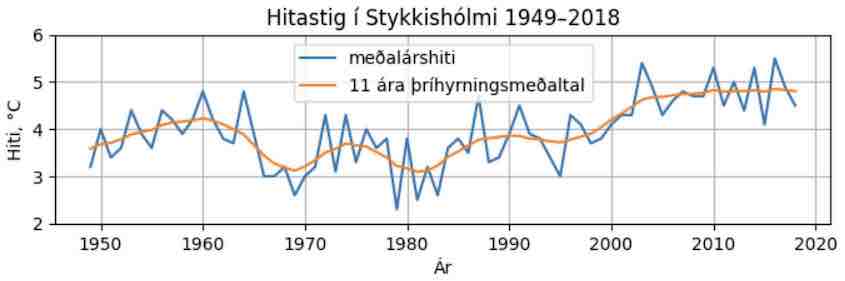
Hér er fall til að reikna svoleiðis hlaupandi meðaltal (ef d er sleppt í kallinu fær það sjálfgefið gildi 5, sem gefur 11 ár).

def hlaupmeðal(x, d=5):
  """skilar lista með hlaupandi (2d+1)-sæta þríhyrn ingsmeðaltali"""
  n = len(x)
  hm = [0]*n
  for i in range(n):
    m = max(0,i-d)
    M = min(n,i+d+1)
    w = [d-abs(k-i) for k in range(m,M)]
    hm[i] = sum([x[m+j]*w[j] for j in range(M-m)])/sum(w)
  return hm

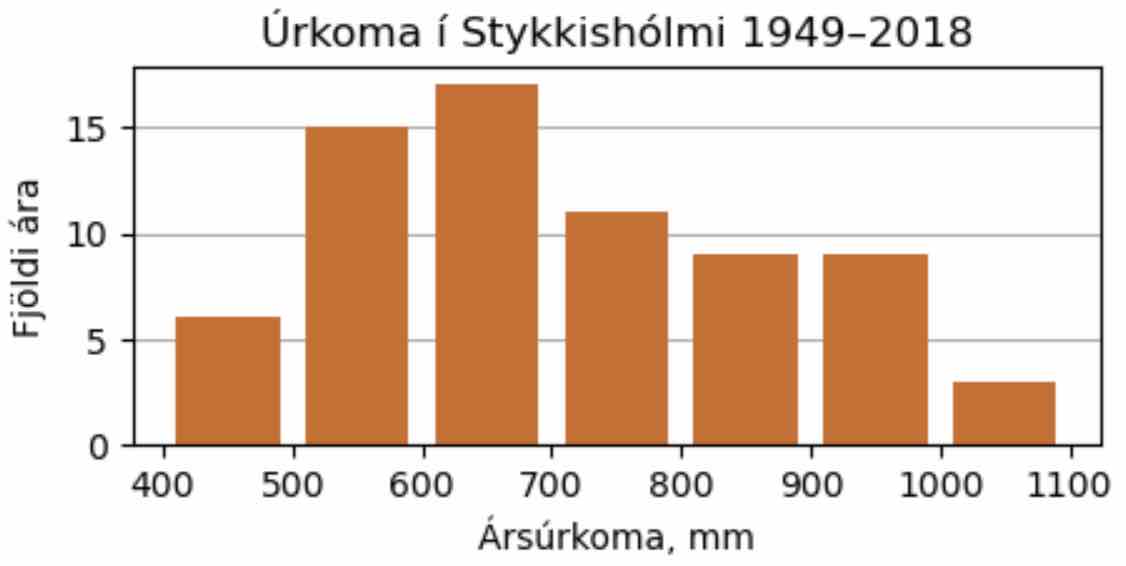
Súlurit af úrkomu Teiknið súlurit af úrkomunni sem lítur nokkurnvegin svona út (myndin er 5x2 tommur og liturinn heitir ‚chocolate‘ en þið megið velja lit að vild):
Punktarit af úrkomu og hita. Teiknið að lokum punktarit (scatter plot) af úrkomu og hita. Byrjið á að fá mynd eins og þá sem er vinstra megin að neðan.

Búið svo til til mynd eins og þá sem er hægra megin með því að láta c-stika í scatter vera lista með ártölum. Kallið loks á plt.colorbar(label="ár") (notið samt ykkar nafn á ártalalistanum) og þá birtist litaskalinn sjálfkrafa.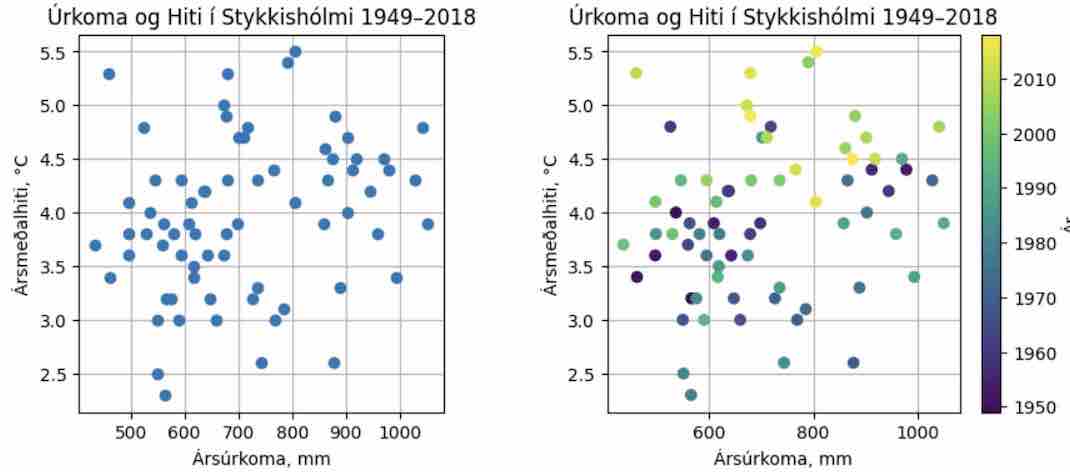
Túlkun niðurstaðna. Búið til textareit og skrifið nokkrar línur um það hvað lesa má út úr myndunum. Bætið gjarna við viðbótarupplýsingum sem fást með útreikningum í Python (t.d. meðalhiti á tilteknum köldum/hlýjum tímabilum, staðalfrávik einhverra valdra stærða, fylgni milli hita og úrkomu).

20 Numpy og vigrar¶

Búið til vigrana \(x = (6,7,18)\) og \(y = (1,1,6)\). Reiknið svo:

\(y - x\)
\(2y + x\)
\((x + y)\cdot(x - y)\)
\(\|x\|^2 - \|y\|^2\)
\(\|x + y\|\cdot\|x - y\|\)

21 Raðað í íslenska stafrófsröð¶

Bæði sorted-fallið og sort-aðferðin sem útskýrð eru köflum 6.1 og 6.5 geta raðað lista af strengjum í enskri stafrófsröð, en því miður lenda séríslenskir stafir ekki á réttum stað í röðinni. Séríslensku stafirnir eru aftast og ekki í réttri röð. Til að laga þetta þarf dálítið stúss. Bæði föllin geta tekið viðbótarviðfang, key sem er fall til að breyta röðinni. Einfalt dæmi er að rita:

L.sort(key=str.lower)

til að raða lista af af strengjum í enska stafrófsröð óháð því hvort þeir hafa lágstafi eða hástafi. Hér er slíkt fall fyrir íslenska stafrófsröð (sem KJ tókst að böggla saman í allmörgum tilraunum). Áhugasamir geta ef þeir vilja stúderað það og e.t.v. lært eitthvað af því (notkunin íslenska.a er kölluð „function attribute“)

def íslenska(s):
    """notað sem 'key' í sort eða sorted til að raða í íslenska stafrófsröð,
    t.d. print(sorted(['ár','bára','bali','akur'], key=íslenska))"""
    return [íslenska.k.get(c.lower(),0) for c in s]
íslenska.a = list('0123456789aábcdðeéfghiíjklmnoópqrstuúvwxyýzþæö')
íslenska.k = dict(zip(íslenska.a, range(1,len(íslenska.a)+1)))

Notið sort eða sorted til að raða listanum ["Ýmir", "Una", "Ása", "Örn", "Þór", "Már", "Mist"], fyrst án þess að nota key (það kemur bandvitlaus röð) og svo með key.
Í skránni https://cs.hi.is/python/kennitolur.txt eru skáldaðar upplýsingar um 15 próftaka, nöfn, prófnúmer og kennitölur, aðskildar með kommum. Lesið skránna inn í þrjá lista annaðhvort með csv-pakkanum (sjá kafla 8.3.2) eða með NumPy. Raðið svo nöfnunum í íslenska stafrófsröð og prentið út, eitt á hverja línu.
Til að fá tilsvarandi prófnúmer og kennitölu aftan við hvert nafn er t.d. hægt að nota uppflettitöflur. Ef L1 og L2 eru jafnlangir listar þá gefur:

tafla = dict(zip(L1, L2))

töflu frá L1 til L2 (sbr. sýnidæmi aftast í kafla 8.2). Búið til slíka uppflettitöflu frá nöfnum yfir í prófnúmer og aðra yfir í kennitölur og skrifið út nýja töflu með þessum upplýsingum, með fyrirsögnum og snyrtilega upp setta (nöfnin enn í stafrófsröð).

22 Sínussveiflur¶

Teiknið góða mynd af fallinu \(f(x) = \sin x + \sin 2x - 2 \sin 3x\) á bilinu \([-\pi, 3\pi]\), sbr. verkefni 18. Hér er dæmi um slíka mynd með ýmsum fídusum.

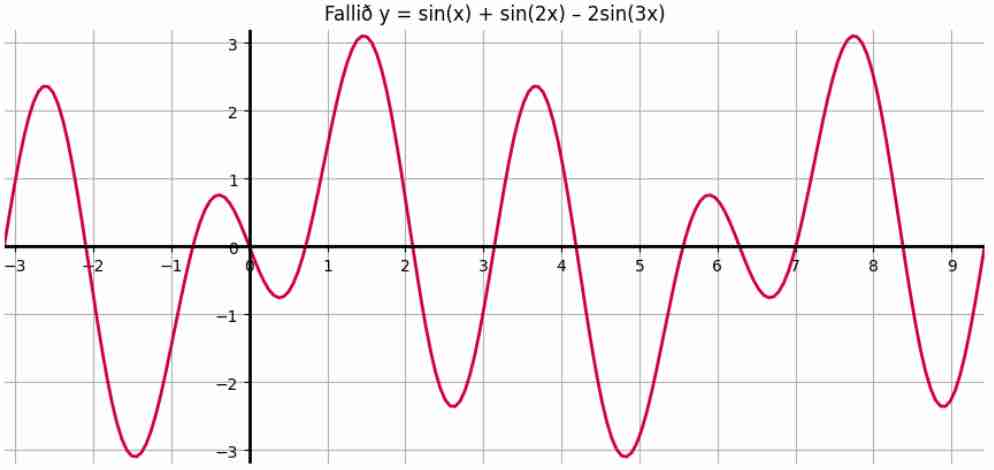
[til að láta ásamerkingarnar koma við ásana sjálfa notaði ég gúgltöfrabrögð: for s in ['left','bottom']: plt.gca().spines[s].set_position('zero')]

23 Málmavinnsla¶

Í lotukerfinu hefur hvert frumefni sætistölu (atomic number), lotu (period) og flokk (group). Sætistalan gefur fjölda rafeinda (electrons) eða róteinda (protons) í óhlöðnu atómi, lotan segir til um hve mörg hvel (atomic orbitals) af rafeindum óhlaðið atóm hefur, en flokkurinn gefur til kynna fjölda rafeinda á ytri hvelum. Fyrir utan helíum eru \(F\) rafeindir á ysta hveli í atómum í flokki \(F\) fyrir \(F = 1, 2\) og \(F - 10\) rafeindir eru þar ef \(11 \leq F \leq 18\). Í flokkum 3–10 er fjöldinn 1–2, oftast 2.

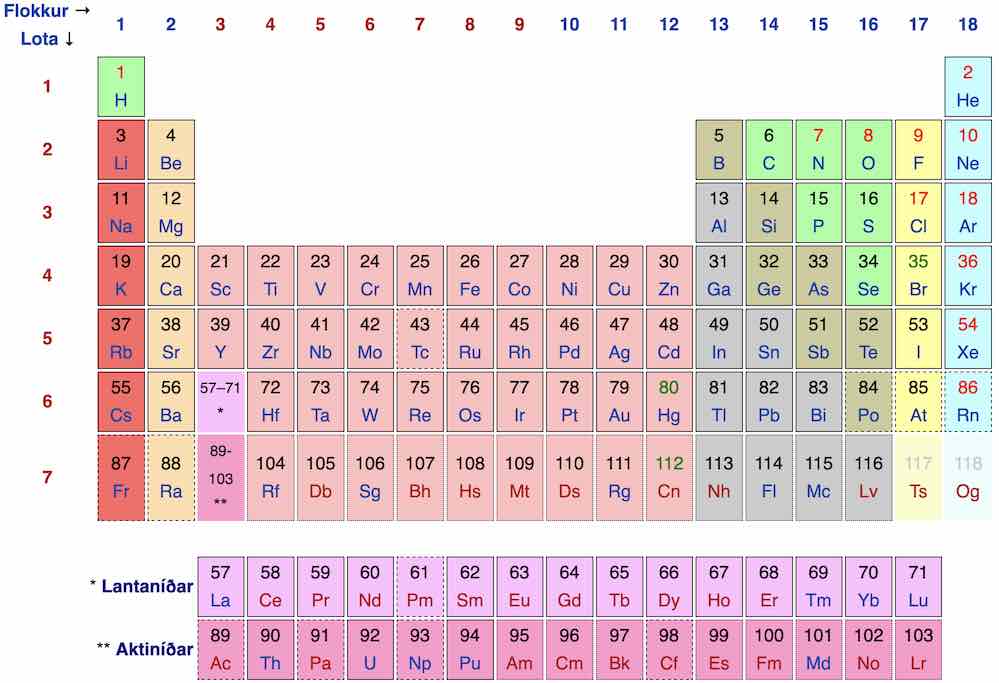
Mynd 23.1: Lotukerfið eins og það birtist á íslensku Wikipedíunni. Á ptable.com er önnur ágæt gagnvirk (interactive) útgáfa.¶

Ysta hvel telst fullskipað ef þar eru 8 rafeindir (2 fyrir helíum). Ef þær eru 1–3 myndar atómið gjarna jákvæða jón, t.d. \(\text{Na}^+\), \(\text{Ca}^{2+}\) eða \(\text{Al}^{3+}\), og ef þær eru 5–7 verður jónin neikvæð, t.d. \(\text{Cl}^–\) eða \(\text{N}^{3–}\). Frumefni með fullskipað ysta hvel, helíum, neon, argon o.s.frv. nefnast eðallofttegundir (noble gases).

Sætistölur eðallofttegunda Hægt er að reikna sætistölu eðallofttegundar nr. \(k\), \(s_k\), með eftirfarandi formúlu:

\[\begin{split}s_k = \dfrac{(k+1)(k+2)(k+3)}{6} + \begin{cases} -2 &\text{ ef }k\text{ er oddatala}\\ \dfrac{k}{2}-1 &\text{ ef }k\text{ er slétt} \end{cases}\end{split}\]

Skrifið fall sem reiknar skv. þessari formúlu og prófið það fyrir \(k=1,2,...,7\). Ath. að allar deilingar ganga upp svo gott er að nota // virkjan svo útkoman verði af heiltölutagi.
Lotur og flokkar Hægt er að ákvarða lotu frumefnis með því að skoða hvar sætistala þess lendir á milli eðallofttegunda. Ef \(s\) er sætistalan og

\[s_{k-1} < s \leq s_k\]

þá er frumefnið í lotu \(k\). Flokkurinn fæst svo með:

\[\begin{split}F = \begin{cases} 1 &\text{ef }s = 1\\ s - s_{k-1} &\text{ef }1 < s \leq s_{k-1} + 2\\ \max(3, 18 + s - s_k) &\text{annars} \end{cases}\end{split}\]

Skrifið föll lota(s) og flokkur(s) sem ákvarða lotu og flokk frumefnis með sætistölu \(s\). Prófið með a.m.k. fjórum frumefnum, þar á meðal einhverjum af sjaldgæfu jarðmálmunum, sem hafa sætistölur á bilinu 57–71 og eru í lotu 6 og flokki 3 skv. lotukerfinu á mynd 23.1. Leiðbeining: Lotuna má finna með while-lykkju og fallinu úr lið 1. Til að finna flokkinn er gott að nota if–elif–else.

Mynd 23.2: Gull og kvikasilfur. Mynd úr bókinni „Efnið“ sem kom út í bókaflokknum „Alfræðasafn AB“ árið 1968.¶
Íslensk og ensk málmanöfn. Með NumPy skipununum í kafla 10.7.3 má lesa skrána https://cs.hi.is/python/allir-malmar.txt inn í vigra efnatákn, nafn, sætistala, eðlisþyngd, bræðslumark og enskt_nafn. Gerið það og búið í framhaldi til uppflettitöflu milli nafnanna með aðstoð dict og zip eins og gert er í sýnidæminu aftast í kafla 8.2 og í verkefni 21c. Náið líka í fallið íslenska úr sama verkefni og notið töfluna og þetta fall til að prenta út orðalista með íslenskum málmanöfnum í stafrófsröð ásamt enskum þýðingum.
Eðlisþyngd eftir sæti. Teiknið punktarit af sætistölu og eðlisþyngd sem er litað með lotu í lotukerfinu (sbr. verkefni 19 – ath. að Matplotlib getur teiknað hvort sem er lista af tölum eða NumPy vigra). Veljið hæfilega punktastærð, bætið colorbar við myndirnar, stillið ásamerkingar eftir smekk, setjið texta við ása og bætið við rúðuneti (grid).
Fleiri myndir Teiknið samskonar myndir af sætistölu og bræðslumarki.

24 Kosningaúrslit í lit¶

Í kafla 9.3.2 var gefið sýnidæmi um einfalda teikningu súlurits af kosningaúrslitum 2021. Þar voru gögnin lesin með aðstoð urlopen, en í þessu verkefni verða þau lesin með NumPy og jafnframt búið til fínna súlurit þar sem:

• súlurnar eru litaðar í flokkslitum
• nöfn flokkanna koma neðan við hverja súlu
• atkvæði eru sýnd í prósentum
• þingsætafjöldi er skrifaður ofan við hverja súlu
• ýmis önnur atriði eru lagfærð

Hér er mynd af súluritinu sem stefnt er að:

Úrslit kosninganna eru í skránni https://cs.hi.is/python/kosningar-2021.txt. Það eru þrír dálkar, með listabókstaf, atkvæðatölu og þingsætafjölda fyrir hvert framboð. Skrána er hægt að lesa með numpy.loadtxt eins og lýst er í kafla 10.7.2. Skrifið fall lesaúrslit() sem les þessa skrá og skilar þremur listum, listi, atkvæði og þingsæti með innihaldinu. Prófið.
Flokkslitina má finna á Wikipedíu sem HEX-strengi, en það er í lagi því Matplotlib skilur það. Litirnir hafa verið lagaðir lítilsháttar og settir ásamt flokksnöfnum í skrána https://cs.hi.is/python/flokkslitir.txt. Þar sem flokksnöfnin innihalda bil eru dálkarnir afmarkaðir með kommum. Skráin er sem sé CSV-skrá og hana má lesa eins og útskýrt er í kafla 10.7.3.

Skrifa skal fall lesalitinöfn sem les skrána og skilar þremur strengjalistum, stafur, litur og nafn með innihaldinu. Það er eitt smá-vesen: Litirnir byrja á # sem NumPy tekur sem comment. Til að það gerist ekki þarf að kalla á loadtxt með

A = np.loadtxt(skrá, ..., comments=None).T

Takið eftir að við notum annað breytunafn fyrir listabókstafina en í lið 1 svo þau ruglist ekki saman. Prófið.
Uppflettitöflur. Í kafla 8.2.5 (og í verkefni 21) er sýnt hvernig auðvelt er að búa til uppflettitöflur úr listum. Hér á að nota tvær töflur til að fletta upp lit og nafni sem svara til listabókstafs:

litatafla: listabókstafur \(\longrightarrow\) litur
nafnatafla: listabókstafur \(\longrightarrow\) flokksnafn

Skrifið fall sem býr til þessar töflur og skilar svo tveimur listum þar sem búið er að fletta upp í þeim. Kallið á fallið á að vera:

(litir, nöfn) = litirognöfn(listi,stafur,litur,nafn)

Þegar búið er að búa til litatöfluna má nota yfirgrip (comprehension) til að búa til litalistann:

litir = [litatafla[st] for st in listi]

og eins fyrir nöfnin. Prófið.

[Athugið að það eru 11 stök í vigrunum með kosningaúrslitunum, en 14 í vigrunum sem koma úr lið 2. Hins vegar verða vigrarnir litir og nöfn bara með 11 stökum, því við flettum bara upp á stöfunum í listi sem hefur lengd 11.]
Einfalt súlurit. Nú er auðvelt að búa til fyrstu útgáfu litaða súluritsins. Náð er í nauðsynleg gögn með því kalla á föllin sem búin voru til í liðum 1–3. Svo er fjöldi súlna og staðsetning þeirra á x-ás fundin með n = len(listi) og x = range(n). Þá má teikna með:

plt.bar(x, atkvæði, color = litir)
Fullgert súlurit. Nú á smám saman að bæta atriðum við súluritið til að fullgera það. Stækkið myndina með því að nota dpi í plt.figure. Atkvæðahlutfallið er auðvelt að reikna í NumPy með því að deila summu atkvæða upp í atkvæðavigurinn: hlutfall = atkvæði/sum(atkvæði) og nota svo hlutfall í staðinn fyrir atkvæði í plt.bar-skipuninni. Til að fá það sem prósentur má kalla á eftirfarandi (töfra)fall.
```
def prósentuformat(ás):
   """merkir ás ("x" eða "y") með prósentum"""
   from matplotlib.ticker import FuncFormatter
   ásar = plt.gca() # get current axes
   xy = ásar.xaxis if ás=="x" else ásar.yaxis
   xy.set_major_formatter(FuncFormatter('{0:.0%}'.format))
```
Flokkanöfnin eru sett neðan við hverja súlu með xticks-skipun eins og í sýnidæminu í kafla 9.3.2, en hinsvegar þarf að skrifa þau lóðrétt, og það er gert með viðfangi rotation, nánar tiltekið:

plt.xticks(x, nöfn, rotation="vertical")

Þá er eftir að skrifa inn þingsætin. Til þess er notuð skipunin text, sbr. töflu 9.2 og líka fyrra sýnidæmið í kafla 9.3.2. Við förum í lykkju yfir x-hnitin í vigrunum og skrifum hvern þinsætafjölda ofan við sína súlu, t.d. í 13 punkta letri. Vigurinn hlutfall gefur y-hnit fyrir textana.

Þá er bara eftir síðsta töttsið. Stækkum y-ás með plt.ylim(...), bætum við titli, skýringu við y-ás, láréttum netlínum með plt.grid(axis="y"). Mestu snyrtipinnarnir losa sig að lokum við tick-merkin með plt.tick_params(length=0).

25 Jafna bestu línu¶

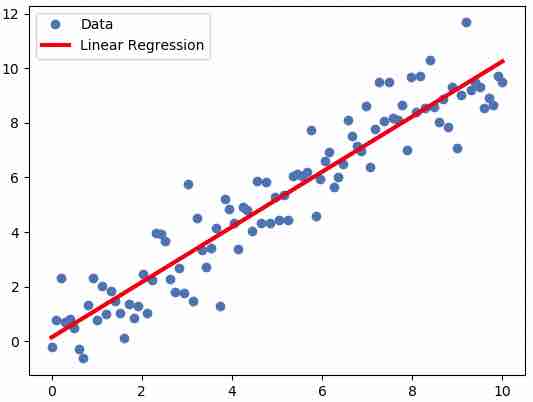
Oft er línulegt samband á milli gagna, þannig að breytur stækka samhliða, en þó með ákveðinni skekkju, sbr. myndina hér til hliðar.

Með aðferð minnstu kvaðrata (linear least squares method) er fundin jafna bestu línu með því að lágmarka kvaðratsummu fjarlægða milli línunnar og gefins punktasafns, eins og lesa má um á Wikipedíu. Það er líka hægt að finna jöfnu bestu parabólu eins og sýnt er aðeins aftar í sömu Wikipedíugrein.

Eftirfarandi skipanir:

(a,b) = np.polyfit(u, v, deg=1)
(A,B,C) = np.polyfit(u, v, deg=2)

skila stuðlum í jöfnu bestu línu og jöfnu bestu parabólu fyrir punktasafnið \((u_0, v_0), (u_1, v_1)\ldots\), þannig að jöfnur línunnar og parabólunnar eru:

\[\begin{split}y &= a x + b \\ y &= A x^2 + B x + C\end{split}\]

Til að teikna línuna eða parabóluna er hægt að nota aðferðir kafla 9.6, en reyndar er hægt að einfalda málið með því að notfæra sér numpy reikninga. Til teikna línuna á bilinu \([x_\text{min}, x_\text{max}]\) má t.d. nota:

xp = np.linspace(xmin, xmax)
yp = a*xp + b
plt.plot(xp,yp,...)

Reyndar þyrfti ekki nema tvo punkta á línunni, til dæmis xp = np.linspace(xmin, ymin, 2) (eða xp = np.array([xmin,ymin])), en parabólan þarf fleiri punkta.

Skoðið framangreinda Wikipedugrein.
Í verkefni 19e voru teiknaðar myndir af meðalárshita og ársúrkomu í Stykkishólmi 1949–2018. Gögnin eru í skránni cs.hi.is/python/hiti-urkoma.txt og þau má lesa inn í þrjá vigra með:

(ár, hiti, úrk) = np.loadtxt("https://cs.hi.is/python/hiti-urkoma.txt").T

Gerið það og ákvarðið jöfnu bestu línu fyrir hita á x-ás og úrkomu á y-ás. Teiknið bæði gögn og línu inn á sömu mynd. Látið myndina hafa stærð (12,6).
Teiknið nú punktarit af ári og ársmeðalhita, og teiknið inn á hana bæði bestu línu og bestu parabólu. Setjið inn hæfilegar merkingar, m.a. ramma með legend-skýringum.

26 Reikningar með NumPy¶

Gefnir eru eftirfarandi vigrar og fylki:

\[a = (3,2,8),\quad b = (2,0,1), \quad c = (-2,1,5)\]

\[\begin{split}A = \begin{pmatrix}2&4&7\\3&4&8\\4&6&9\end{pmatrix} \quad\text{og}\quad B = \begin{pmatrix}5&5&5\\6&6&6\\7&8&9\end{pmatrix}\end{split}\]
1. Finnið \(a\cdot b - \dfrac{c\cdot(Bb)}{3\|c\|}\)
2. Finnið \(2(A^\text{T} + B^2)(a - 2b)\)
3. Ákvarðið \(\det(A)\) og \(A^{-1}\)
4. Leysið jöfnuhneppið \(Ax = b\)
5. Palli er með fimmkalla og tíkalla í vasanum, alls 23 peninga, samtals 170 kr. Hvað er hann með mikið af hvorri mynt?
Skrifið fall til að leysa jöfnurnar:

\[\sum_{j=0}^{i-1}(i-j)x_j + x_i = 2\quad (i=0,1,\ldots,n-1)\]

sbr. sýnidæmi og æfingu í kafla 11.4. Prófið með n = 4 (ætti að gefa \(x=(2,0,-2,-2)\)

27 Körfuboltamenn¶

Skráin cs.hi.is/python/karfa.txt inniheldur þrjá dálka með aldri hæð og þyngd 1064 bandarískra körfuboltamanna. Notið np.loadtxt til að lesa skrána inn í þrjá vigra t.d. aldur, hæð og þyngd eða a, h og þ. Eftirfarandi teikningar þarf að gera sæmilega snyrtilega, m.a. merkja ása og setja inn titla og passa að þær séu mátulega stórar. Mörk súlna í súluritunum þurfa að vera rúnnaðar tölur (t.d. heilar eða hálfar tölur) og súlurnar eiga að hafa bil á milli sín. Þeir sem vilja mega setja einhverjar teikningar hlið við hlið með því að nota plt.subplot, sbr. kafla 13.5 og einfalda lýsingu hjá w3schools.

Teiknið þrjú súlurit af aldri, hæð og þyngd.
Teiknið punktarit með hæð á x-ás og þyngd á y-ás. Finnið svo og teiknið jöfnu bestu línu inn á myndina (sbr. verkefni 25)
Teiknið aðra mynd með bestu parabólu.
Miðtölu (median) vigurs x má finna með np.median(x) (helmingur staka x er minni en miðtalan og helmingur stærri). Hver er miðtala aldurs körfuboltamannanna. Notið miðtöluna til að skipta gögnunum í tvennt (með rökvísun), yngri og eldri. Finnið meðalhæð þeirra yngri og þeirra eldri.

28 Kínverskt jöfnuhneppi¶

Hér er dæmi úr gömlu kínversku handriti frá því á fyrstu öld f.Kr. Leysið það með NumPy:

Nokkrir ætla að leggja í púkk til að kaupa hlut. Ef hver borgar átta peninga eru þrír peningar afgangs en ef hver borgar sjö vantar fjóra upp á. Hve margir eru kaupendur og hvað kostar hluturinn?

29 Fjarlægð milli borga¶

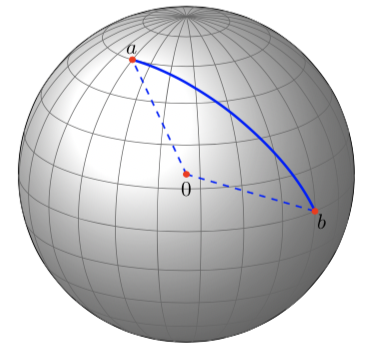
Ef sett er hnitakerfi í gegn um miðju jarðar þá verður þrívíður vigur sem byrjar í miðjunni og endar á stað á yfirborðinu með lengd \(l\) og breidd \(b\):

\[\begin{split}\pmatrix{R\sin l \cos b\\R\cos l \cos b\\R\sin b}\end{split}\]

þar sem \(R\) er radíus jarðar, \(R \approx 6370\ \text{km}\). Í stærðfræðigreiningu eru \(R\), \(l\) og \(b\) kölluð kúluhnit (spherical coordinates). Hnattstaða Reykjavíkur er u.þ.b. 64°N og 22°W, og hattstaða London u.þ.b. 51.5°N og 0°W.

Horn \(\theta\) milli vigra \(x\) og \(y\) má reikna með:

\[\theta = \arccos\frac{x\cdot y}{\|x\| \|y\|}\]

Reiknið hornið milli Reykjavíkur og London mælt frá miðju jarðar.
Lengd hringboga í hring með radíus \(r\) sem spannar horn sem er \(\theta\) radíanar er

\[L = \theta r\]

(sbr. hringbogi á Wikipediu. Reiknið fjarlægðina milli Reykjavíkur og London (Siri segir 1890 km)

Munið að það þarf að breyta gráðum í radíana og öfugt með math.radians og math.degrees (eða np-útgáfum af þessum föllum)

30 Æfing í tölvugrafík¶

Til að teikna flatarmynd sem lýst er með \(2\times n\) fylki (sbr. kafla 12.1) og til að hliðra slíkri mynd má nota eftirfarandi föll:

def teikna_fylki(A):
   # Teiknar 2 x n flatarmyndarfylki
   plt.plot(A[0],A[1], lw=3, color='k')

def hliðra(A, h):
   # Leggur h við alla dálka A
   return A + np.reshape(h,(2,1))

Seinna fallið notar það trix að byrja á að breyta h í 2×1 fylki, og afgangurinn gerist sjálfkrafa. Þegar tölvuteikning er hugsuð sem teikning af myndum í hnitakerfi fer oft best á að láta einingar á x- og y-ás vera jafnar. Það fæst með skipuninni plt.axis("equal") (sem er því miður ekki hægt að setja í byrjunarreit–það er eiginlega Matplotlib-lús)

Hér er vinnubók sem nota má til að leysa eftirfarandi verkefni:

Flatarmynd lýst með 2xn fylki. Búið til fylkið

\[\begin{split}M = \begin{pmatrix} 0 & 3 & 3 & 0 & 0 & \text{nan} & 1 & 2 \\ 0 & 0 & 2 & 2 & 0 & \text{nan} & 1 & 1 \end{pmatrix}\end{split}\]

og teiknið myndina sem það lýsir (rétthyrningur með striki). Notið svo 30°-skekkingarfylki til að breyta honum í samsíðung og teiknið hann.
Snúningsfylki. Skrifið fall sem skilar snúningsfylki fyrir almennt horn og snúningspunktinn \((0,0)\). Notið það til að snúa rétthyrningnum í lið 1 og teiknið útkomuna.
Sammiðja rétthyrningar. Búið til fylki fyrir rétthyrning sem er 5 x 3 að stærð með minni rétthyrning sem er 3 x 1 að stærð í miðjunni (stærri rétthyrningurinn hefur neðra vinstra horn í \((0,0)\) en sá minni í \((1,1)\)). Teiknið myndina sem kemur út með teikna_fylki.
Þríhyrningur með hæð. Búið til fylki T sem lýsir þríhyrningi með hornpunkta \(A = (1,0)\), \(B = (3,2)\) og \(C = (4,0)\) með lóðréttu striki (hæð) frá \(B\) niður á hliðina \(AC\). Teiknið.
Hliðra–snúa–hliðra. Búið til fall sem notar snúningsfylkisfallið úr lið 2 ásamt fallinu hliðra til að snúa um almennt horn og almennan punkt. Notið það til að snúa þríhyrningnum í lið 4 um 180° um punktinn \(B\) og teiknið bæði upphaflega þríhyrninginn og þann snúna inn á sömu mynd.
Snúa–spegla–snúa. Búið nú til fall sem skilar fylki sem speglar um gefna línu \(y = ax\) með því að snúa, spegla og snúa til baka (notið fylkjamargföldun). Hornið sem línan myndar við x-ás fæst með \(\arctan a\). Prófið að spegla þríhyrningnum í lið 4 um línuna \(y = x\).

Athugið: Í lið 2 skilar fallið snúningsfylki (t.d. R), og svo má margfalda myndafylki með því til að snúa myndinni (t.d. teikna_fylki(R @ mynd). Sama framgangsmáta má nota í lið 6, en í lið 5 þarf myndafylkið að vera stiki (t.d. hiðra_snúa_hliðra(mynd, horn, punktur) því ekki er hægt að skeyta saman hliðrun og margföldun saman í eina fylkjaaðgerð.

31 Flæðinet¶

Stefnt net hefur 5 hnúta og eftirfarandi 7 leggi:

• frá hnút 1 til 2 og 3
• frá 2 til 3 og 4
• frá 3 til 4 og 5
• frá 4 til 5

(til að leysa með blaði og blýanti)
1. Teiknið netið
2. Finnið grannafylkið \(A\)
3. Finnið legufylki netsins, \(L\), miðað við að leggirnir séu tölusettir í sömu röð og þeir eru taldir upp að ofan.
4. Lát burðargetu leggjanna vera sem hér segir:
  
  leggur
  
  burðargeta
  
  1–2
  
  5
  
  1–3
  
  5
  
  2–3
  
  4
  
  2–4
  
  3
  
  3–4
  
  2
  
  3–5
  
  3
  
  4–5
  
  5
  
  Reiknið hámarksflæði með Ford-Fulkerson aðferðinni og blaði og blýanti. Byrjið með veginn 1–2–4–5, svo 1–3–5 og loks 1–3–4–5 og sýnið flæðið eftir hvert skref. Hvert er flæðifylkið eftir lokaskrefið (þ.e. fylki með \((i,j)\)-stak jafnt flæðinu í legg \(i \to j\))?
(til að leysa með Python)
1. Reiknið \(A^2\) og \(A^3\) og ákvarðið í framhaldi heildarfjölda mismunandi vega með lengd 3 í netinu
2. Notið fylkjaveldi og samlagningu til að finna heildarfjölda vega frá 1 til 5
3. Notið maximium_flow fallið í SciPy til að finna hámarksflæði og tilsvarandi fylki, sbr. lið 1d.
4. Gerum nú ráð fyrir að það flæði 2 l/s í öllum leggjum nema 4–5, þar flæði 4 l/s. Notið flæðisvarðveislujöfnuna til að ákvarða hvaða hnútar eru lindir og ósar og hve mikið streymir inn og út þar.

32 Leslie-fylki fyrir fjögur ár¶

Liði 1 og 2-1 má leysa hvort sem er með NumPy eða á blaði, en fyrir liði 2-2 og 2-3 borgar sig líklega að nota NumPy. Tegund nokkur nær mest 4 ára aldri og verður kynþroska 1 árs. Að jafnaði eignast hver eins árs, annar hver tveggja ára, og þriðji hver þriggja ára eitt afkvæmi. Helmingur núll ára, 70% eins árs og 40% tveggja ára lifa til næsta árs (en sem sé enginn þeirra sem eru þriggja ára). Í upphafi eru 1000 núll ára, 1000 eins árs og 1000 tveggja ára, en aðeins 500 þriggja ára.

Finnið Leslie fylkið.
1. Hver er stofnstærðin eftir eitt ár?
2. Hver er stofnstærðin eftir 10 ár?
3. Fjölgar í það óendanlega eða deyr stofninn að lokum út?

33 Leslie-fylki og gröf¶

Tegund lifir að hámarki í 5 ár. Fæðingartíðni og dánartíðni og upphafleg aldursdreifing er sem hér segir:

aldur	fæðingartíðni	dánartíðni	fjöldi
0–1	0.1	0.1	100
1–2	0.3	0.1	200
2–3	0.5	0.2	300
3–4	0.4	0.4	200
4–5	0.1	1.0	200

Búið til Lesley-fylki (með NumPy) og ákvarðið stofnstærð í byrjun og á hverju ári næstu sjö ár.
Mun stofninn að lokum deyja út?
Teiknið mynd af fæðingar- og dánartíðninni á þessa leið (línubreidd er 3 punktar):
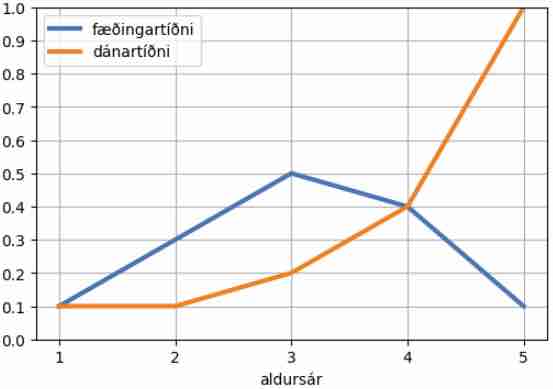
Teiknið mynd af þróun stofnstærðarinnar næstu 20 ár

34 Mannfjöldaspá fyrir Ísland¶

Í skránni https://cs.hi.is/python/aldursdreifing.txt eru gögn um mannfjölda á Íslandi árið 2020, fæðingartíðni og dánartíðni, og fjölda aðfluttra umfram brottflutta eftir aldri.

Notið Leslie-fylki til að spá mannfjölda á Íslandi 2020–2075 ef ekki er tekið tillit til innflytjenda. Skrifið töflu yfir heildarfjöldann á 5 ára fresti.
Bætið við áhrifum innflytjenda ef gert er ráð fyrir að árlegur fjöldi aðfluttra umfram brottflutta á hverjum aldri haldist óbreyttur.
Teiknið súlurit af aldursdreifingunni í byrjun og lok tímabilsins miðað við niðurstöðu úr 2. lið (eða 1. lið ef þið sleppið 2. lið). Teiknið líka línurit af heildarmannfjöldanum (með ár á x-ás).
Breytið spánni ef reiknað er með að hlutfallslegur fjöldi aðfluttra umfram brottflutta á hverjum aldri sem hlutfall af heildarmannfjöldanum haldist óbreyttur. Teiknið þrjú línurit af af heildarmannfjöldanum skv. liðum 1, 2 og 4 inn á sömu mynd.
Búið til textareit og skrifið nokkrar (t.d. 10) línur um niðurstöðurnar frá eigin brjósti. Hafið einhverjar tölulegar upplýsingar fengnar með Python með og sömuleiðis eitthvað sem þið finnið með leit á netinu. Það eru viljandi ekki gefin frekari fyrirmæli heldur er ætlast til að þið notið hugmyndaflugið.

Athugasemd:

Tölurnar í textaskránni eru búnar til með upplýsingum af vef Hagstofu Íslands með smávegis föndri. Eins og segir er mannfjöldinn miðaður við árið 2020 en hinar tölurnar eru 5 ára meðaltal.

35 Póker¶

Hér er reitur með (hluta af) lausn á æfingunni í kafla 13.1, sem metur með hermun líkurnar á því að fá tvær tvennur í póker. Fallið pókerhönd er endurbætt miðað við æfinguna til að tryggja að sama spil geti ekki komið fyrir tvisvar. Fræðilegar líkur á tveimur tvennum er 4.75% og ef keyrt er með háu gildi á n fæst hlutfall nálægt því.

from random import sample

def pókerhönd():
  stokkur = [(i,j) for i in range(1,5) for j in range(1,14)]
  return sample(stokkur, 5)

def með_tvær_tvennur(hönd):
  # Skilar sönnu ef hönd geymir tvær tvennur
  gildi = [spil[1] for spil in hönd]
  M = set(gildi)                 # búa til mengi
  if len(M) != 3:
    return False                 # það verða að vera 3 gildi
  for spil in M:
    talning = gildi.count(spil)
    if talning > 2: return False # og ekkert spil má koma 3svar
  return True                    # það eru tvær tvennur!

def hlutfall_með_2x2(n):
  talning = 0
  for i in range(n):
    hönd = pókerhönd()
    if með_tvær_tvennur(hönd):
      talning += 1
  return talning/n

hf = hlutfall_með_2x2(100000)
print(f'Hlutfall með tvær tvennur: {hf*100:.1f}%')

Mynd 35.1: Fullt hús¶

Í lausninni er spil er táknað með pari (sort, gildi) þar sem sortin er á bilinu 1–4 (hjarta, spaði, tígull, lauf) og gildi er á bilinu 1–13 (ás, tvistur,…, kóngur).

Skrifið föll sem kanna hvort hönd geymi:

tvennu

þrennu

fullt hús (3 + 2)

lit (t.d. eintómir spaðar)

Hermið slíkar hendur og berið saman við raunverulegar líkur fengnar af netinu.

36 Stærð jarðskjálfta¶

Stærð jarðskjálfta (nánar tiltekið vægisstærð, moment magnitude) er gefin með formúlunni

\[M = \frac{2}{3}(\log_{10} M_0 - 9.1)\]

þar sem \(M_0\) er heildavægi (orka) skjálftans í newtonmetrum (Nm) og \(\log_{10}\) er logri með grunntölu 10.

Skrifið fall sem reiknar (og skilar) stærð jarðskjálfta fyrir gefið vægi. Hafið skjölunarstreng með. Prófið með \(M_0 = 10^{16}\), sem á að skila \(M = 4.6\).
20. október 2020 varð stór jarðskjálfti nálægt Krýsuvík. Á netinu má finna þrjár mælingar á orku skjálftans frá þremur alþjóðlegum jarðskjálftamiðstöðvum:

Miðstöð

Land

\(M_0\)

USGS

Bandaríkin

\(3.20 \cdot 10^{17}\)

GCMT

Bandaríkin

\(3.29 \cdot 10^{17}\)

GFZ

Þýskaland

\(2.90 \cdot 10^{17}\)

Skrifið forrit sem býr til uppflettitöflu stærð með orku jarðskjálftanna skv. miðstöðvunum þremur (þannig t.d. að stærð["USGS"] sé 3.20e17), og skrifar í framhaldi út töflu yfir niðurstöðuna sem byrjar svona:
```
Miðstöð   Stærð
–––––––––––––––
USGS      5.60
...
```

37 Valkvæðir stikar¶

Föll geta haft valkvæða stika sem taka sjálfgefin gildi ef þeim er sleppt. Þannig hefur print-fallið tvo valkvæða stika, sep og end, sbr. kafla 4.4. Eftirfarandi dæmi, sem reiknar n-tu rót, sýnir hvernig hægt er að skilgreina fall með valkvæðan stika. Fallið reiknar kvaðratrót ef seinna viðfanginu er sleppt og prentar því út rætur: 4 og 2. Annað dæmi er í verkefni 19.3.

import math
def rót(x, n=2):  # skilar n-tu rót (n=2 er sjálfgefið)
   return x**(1/n)

a = rót(16)
b = rót(16, 4)
print(f"rætur: {a} og {b}")

Skrifið svona fall fyrir logra (logarithm) með grunntölu \(a\) skv. formúlunni:

\[\log_a(x) = \frac{\ln x}{\ln a}\]

þar sem \(ln\) er náttúrulegi logrinn, sem í Python er reiknaður með math.log(x). Látið a vera valkvæðan stika með sjálfgefið gildi 10. Prófið að reikna \(\log_{10}(100)\), \(\log_3(243)\) og \(\log_{2}(128)\) sem ætti að gefa 2, 5 og 7.
Skrifið fall sem prentar lista af tölum með nauk stöfum fyrir aftan kommu með nauk = 4 sjálfgefið. Ef það fær listann:

[[math.exp(x) for x in range(6)]

og nauk = 3 ætti það að prenta út [1.000, 2.718, 7.389, 20.086, 54.598, 148.413].

38 Dæmi af prófi í Tölvunarfræði 1a 2020¶

(þetta eru öll dæmin sem voru á prófinu, hvert þeirra gilti 20%)

A. Efnisspurningar

Gerið í stuttu máli grein fyrir hugtökunum viðfang (argument) og stiki (parameter), bæði með skilgreiningum og dæmi.
Segið frá listum og samstæðum (tuples): hverning má búa til lista og samstæðu og hvað felst í að listar eru breytanlegir en samstæður ekki. Útskýrið hvernig nota má par (samstæða tveggja gilda) til að láta fall skila tveimur niðurstöðum (t.d. með dæmi). Nefnið tvær aðgerðir sem beita má á lista en ekki samstæður.
Útskýrið, t.d. með dæmum, muninn á aðgerðunum + og * þegar þeim er beitt á a) Lista, b) NumPy vigra
[ATH: Þetta dæmi er úr námsefni sem er ekki (enn) í fyrirlestrarnótunum]. Gerið grein fyrir hugtakinu endurkvæmt fall (recursive function). Skilgreinið það, segið frá hvernig komið er í veg fyrir að forrit með endurkvæmu falli keyri endalaust, og gefið dæmi um endurkvæmt fall.

B. Vaxtareikningur

Skrifið fall með stika u, p, k, m sem reiknar heildarvexti, \(v\), af upphæð \(u\) sem er á \(p\)% vöxtum í \(k\) ár og \(m\) mánuði skv. formúlunni

\[v = u(1 + a)^k\left(1 + \frac{am}{12}\right) - u \text{, þar sem }a = \frac{p}{100}\]

Skerið af aura (með fallinu int), hafið viðeigandi skjölunarstreng í fallinu, og prófið það með því að reikna 2% vexti af 10000 kr. í 3 ár og 4 mánuði (ætti að gefa 682 kr.).
Reiknið heildarvexti til dagsins í dag ef 25000 kr. hefðu verið lagðar inn á 3% vexti á fæðingardegi ykkar (nálgið aldur ykkar í heilan mánuð), og reiknið jafnframt út hlutfall vaxtanna af upphaflegri upphæð. Notið f-strengi til að skrifa niðurstöðurnar með hæfilegum skýringartexta.
Skrifið fall sem ákvarðar hve mörg ár og mánuði það tekur upphæð á \(n\)% vöxtum að tvöfaldast (notið t.d. tvöfalda lykkju, og return á viðeigandi stað). Prófið með n = 13 (ætti að gefa 5 ár og 8 mánuði) og með \(n\) gefnu með fæðingarmánuði ykkar (t.d. 8 fyrir ágúst).

C. Kennitölur og vartöluprófun

Skv. Wikipediu er kennitala númer á forminu DDMMÁÁ-NNPÖ þar sem DDMMÁÁ er fæðingardagur, -mánuður og -ár, NN er slembitala, P er prófsumma eða vartala, og Ö táknar fæðingaröld. Til að finna vartöluna eru fyrstu átta tölurnar margfaldaðar með tölunum 3, 2, 7, 6, 5, 4, 3 og 2 frá vinstri til hægri, margfeldin eru svo lögð saman og afgangur þegar deilt er í summuna með 11 fundinn. Ef afgangurinn er 0 er vartalan 0, ef hann er 1 er talan ónothæf sem kennitala, en annars fæst vartalan með því að draga afganginn frá 11.

Skrifið fall sem ákvarðar hvort kennitala sem gefin er með 10 stafa streng (án bandstriks) sé með rétta vartölu og skilar svarinu sem rökgildi (True eða False). Prófið með "9999999999" og líka með eigin kennitölu.
Í skránni https://cs.hi.is/python/kennitolur.txt eru skáldaðar upplýsingar um 15 próftaka, prófnúmer, kennitölur og nöfn. Lesið skrána inn í þrjá lista með því að nota np.loadtxt(...) og birtið töflu með innihaldinu.
Vartöluprófið kennitölurnar (í for-lykkju). Ein þeirra stenst ekki prófun. Hvaða nemandi á hana?
Hér er listi yfir mánaðarnöfn:

['janúar', 'febrúar', 'mars', 'apríl', 'maí', 'júní', 'júlí', 'ágúst', 'september', 'október', 'nóvember', 'desember'].

Skrifið fall sem tekur við kennitölu og skilar tilsvarandi fæðingardegi með sniði: „17. ágúst 1958“. Prófið með eigin kennitölu, og líka kennitölu einhvers í skránni sem fæddur er á annari öld.

D. Uppflettitöflur

Lesið skrána sem notuðu var í dæmi C inn í þrjá lista eins og gert var þar.

Búið til uppflettitöflu (dictionary) til að fletta upp á prófnúmeri út frá nafni (nafn er lykill og prófnúmer er gildi).

Skrifið forrit sem skrifar út lista (með haus) yfir nöfn og prófnúmer í íslenskri stafrófsröð. Listinn gæti byrjað svona:

NAFN                         PRÓFNÚMER
Anton Ingi Þórsson             4854
Ágúst Guðni Ingason            6558

Leiðbeining: Notið uppflettitöfluna úr lið 1. Hér á eftir er svo fall sem nota má fyrir röðunina (með því að nota key=íslenska sem viðfang í sort eða sorted, sjá verkefni 21).

def íslenska(s):
   # notað sem 'key' í sort eða sorted til að raða í íslenska stafrófsröð,
   # t.d. print(sorted(['ár','bára','bali','akur'], key=íslenska))"""
   return [íslenska.k.get(c.lower(),0) for c in s]
íslenska.a = list('aábcdðeéfghiíjklmnoópqrstuúvwxyýzþæö')
íslenska.k = dict(zip(íslenska.a, range(1,len(íslenska.a)+1)))

Hér er listi yfir prímtölur númer 1 til 25:
```
P = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
```
Búið til uppflettitöflu, nrp, sem hægt er að nota til að fletta upp hvar gefin prímtala er í röðinni. Ef flett er upp á lyklinum P[i] á að fást gildið i+1 (ekki i af því Python byrjar að telja í 0). Notið for-lykkju sem rennir í gegn um P til að búa til uppflettitöfluna. Skrifið í framhaldi fall með tvo stika, tölu og nrp. Ef talan er stærri en 99 á fallið að skrifa að hún sé of stór, en annars á það að fletta upp í uppflettitöflunni og skrifa niðurstöðu uppflettingarinnar. Ef tölunum 13, 16 og 103 er flett upp gæti komið út:
```
13 er 6. prímtalan
16 er ekki prímtala
103 er of stór
```

E. Teikning falla

Notið Matplotlib til að teikna feril fallsins:

\[f_a(x) = \frac{(2-x)^{2a}\ln(1+x)}{e^{a}}\]

á bilinu \([0,2]\) þegar \(a=8\). Gætið þess að ferillinn verði nægilega sléttur („smooth“), merkið ása með x og y og setjið titil: Teikning falls. Athugið að í Python heitir náttúrulegi logrinn log.
Teiknið nú nýja mynd sem sýnir öll föllin \(f_a(x)\) fyrir \(a = 2, 4, 6, 8\) á bilinu \([0,2]\). Frekari fyrirmæli eru:
- stærð myndar 8 x 4 tommur
- dpi = 100
- myndin skal hafa rúðunet, merkingar á ásum og titil
- legend skal gefa gildi \(a\)
- x-ás skal ná frá 0 til 2 og y-ás frá 0 til 1
- x-hnitin \(0, 0.2,\ldots 2\) á að merkja á ásinn (ticks)

39 Nálgun við pí¶

Eftirfarandi summa gefur Taylor-nálgun við \(\arctan x\) og skekkjan er minni en síðasti liðurinn. Það þýðir að ef \(x=0.2\) þarf að fara upp í \(n \approx 10\) til að fá 15 rétta aukastafi, og til að fá 100 rétta aukastafi þarf \(n\approx 70\).

\[\arctan x \approx x - \frac{x^3}{3} +\frac{x^5}{5} - \frac{x^7}{7} + \ldots + \frac{(-1)^n x^{2n+1}}{2n+1}\]

Skrifið fall tayloratan(x,n) sem reiknar út summuna. Fallið á að vinna með tvær breytur, summu og lið, sem í upphafi eru báðar x. Farið er í gegn um lykkju þar sem k hleypur í gegn um \(3, 5, \ldots, 2n+1\). Í hverri umferð margfaldast liðurinn með \(-x^2\) (liður *= -x*x) og svo er liður/k lagt við summuna. Prófið með \(x=0.2\) og \(n=4\) (ætti að gefa \(0.19739550\)) og \(n=10\) (ætti að gefa rétt gildi með 15 aukastöfum, \(\arctan 0.2 = 0.197395559849881\))
Árið 1706 sannaði John Machin formúlu fyrir pí:

\[\frac{\pi}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239}\]

og notaði hana ásamt arctan-formúlunni að framan til að reikna pí með 100 aukastöfum. Þessi formúla var svo notuð í 275 ár, vel inn á tölvuöld, til að reikna sífellt betri nálgun við pí. Það var hún sem var notuð árið 1949 til að reikna pí með tölvu í fyrsta sinn, 2037 aukastafi með tölvunni ENIAC, og árið 1981 var enn verið að nota Machin-formúluna til að slá nýtt pí-met, 2 milljónir aukastafa.

Python vinnur með kommutölur sem hafa ~16 aukastafi, svo það er fremur auðvelt að nota framangreinda aðferð til að reikna 15–16 aukastafi í pí (en dálítið mál að reikna fleiri). Notið fallið tayloratan og Machin-formúluna til að nálga pí með 15 réttum aukastöfum.

40 Pandas æfing¶

Í skránni https://cs.hi.is/python/kosningar-2021.txt eru úrslit nýjustu Alþingiskosninga (eftir endurtalningu í NV-kjördæmi), og í skránni https://cs.hi.is/python/flokksnofn.txt eru listabókstafir í fyrsta dálki og þar fyrir aftan eru nöfn flokkanna, sem geta verið tvö eða fleiri orð. Fyrri skrána er auðvelt að lesa með pd.read_fwf en þá seinni er líklega auðveldast að lesa með pd.read_csv og viðfangi sep=",\t" (það eru tab-tákn á eftir kommunum í skránni).

Lesið kosningaúrslitin og birtið þau.
Lesið seinni skrána, sameinið við fyrri skrána (með df.join) og birtið kosningaúrslitin með flokksnöfnum.
Bætið við dálki með hlutfalli atkvæða sem hver flokkur fékk og birtið svo nýja töflu yfir þá flokka sem fengu meira en 5% (og komu þar með manni á þing).

41 Dýraklasi¶

Búið til afstrakt klasa Dýr. Klasinn á að hafa klasabreytur tegund (strengur), fótafjöldi (heiltala), og segir (strengur, t.d. "voff"), og klasaaðferð segja sem á að skrifa tvisvar á skjáinn hvað dýrið segir (t.d. "voff voff", "me me"). Klasabreytur fá gildið None. Klasinn á líka að hafa eiginleika nafn (strengur) og litur (strengur). Ennfremur á klasinn að hafa smið og útskriftaraðferð __str__. Útskriftaraðferðin gæti t.d. skrifað út „Snúlla er bröndótt kisa“ (eftir að búið er að búa til kisuklasa sem erfir frá Dýr).
Búið til (konkret) klasa Hundur sem erfir frá klasanum Dýr. Hann hefur smið sem kallar á smið yfirklasans og aðferð gelta sem kallar á segja í yfirklasanum. Það þarf líka að gefa klasabreytunum þremur viðeigandi gildi. Búið svo til tilvik af hundi sem heitir Snati og er svartur. Prentið hann út ásamt fótafjöldanum og látið hann gelta. Búið líka til klasa Önd með aðferð kvaka og prófið með sama hætti. Forritið ætti að skrifa út eitthvað á þessa leið:
```
Snati er svartur hundur
Hann hefur 4 fætur
voff voff

Andrés er brún önd
Hún hefur 2 fætur
bra bra
```

Ef forritað er eins og hér hefur verið lýst er ekkert sem kemur í veg fyrir að búin sé til hlutur af taginu Dýr, í andstöðu við tilganginn með afstrakt klösum. Byrjið á að skoða Wikipedíugreinina um þá og sömuleiðis eitthvað um Python pakkann abc (abstract base classes); mér sýnist þessi síða einföld og skilmerkileg. Leysið svo eftirfarandi:

Sannreynið að það er ekkert mál að búa til dýr af engri sérstakri tegund. Til að fá villu ef reynt er að búa til tilvik af afstrakt klasa þarf hann að vera með a.m.k. eina afstract aðferð. Bætið afstrakt aðferð hreyfast við klasann Dýr sem er bara með eina línu, pass. Látið klasann erfa frá yfirklasanum ABC (eftir from abc import ABC) og látið nýju aðferðina vera afstrakt (með því að setja @abstractmethod framan við hana). Prófið nú að búa til dýr.
Eftir þessar „úrbætur“ er orðið skylda að undirklasarnir útfæri (implement, endurskilgreini) aðferðina hreyfast. Prófið fyrst að búa til hund án slíkrar útfærslu og svo með (hún gæti t.d. skrifað út „Ég get gengið og hlaupið“). Endurtakið fyrir öndina (hún getur gengið, flogið og synt).

Miðstöð	Land	\(M_0\)
USGS	Bandaríkin	\(3.20 \cdot 10^{17}\)
GCMT	Bandaríkin	\(3.29 \cdot 10^{17}\)
GFZ	Þýskaland	\(2.90 \cdot 10^{17}\)