13 Slembitölur¶
Slembitölur (random numbers) koma oft við sögu í forritun. Til dæmis eru þær nauðsynlegur hluti af hermun (simulation) þar sem líkt er eftir raunverulegu ferli eða atburðarás í tölvu, þær eru notaðar til að forrita slembin spil, m.a. teningaspil og spil fyrir venjulegan 52 spila stokk, þær eru mikið notaðar í tölfræðilegri greiningu, og þær nýtast til að búa til gervigögn. Flestöll nútíma-forritunarmál geta búið til slembitölur, og er Python þar engin undantekning. Við höfum þegar kynnst þeim lauslega í köflum 9.2.3, 9.5.2 og 9.5.3 (kíkið gjarnan á þessa kafla).
13.1 Random-einingin¶
Einfaldasta leiðin til að búa til slembitölur er að nota föll úr einingunni random. Með henni er hægt að búa til bæði jafnt dreifðar og normaldreifðar slembitölur (kommutölur), og einnig slembiheiltölur. Til þess má nota föllin random, gauss og randint, svona:
from random import random, gauss, randint
x = random() # skilar slembitölu, 0 ≤ x < 1
k = randint(1,8) # skilar slembiheiltölu,1 ≤ k ≤ 8
K = [randint(5,7) for i in range(9)] # skilar 10 slembiheiltölum í {5,6,7}
z = gauss(1,3) # z er normaldreift með meðalgildi 1
# og staðalfrávik 3, ritað z ~ N(1,3)
Nafnið gauss kemur til vegna þess að normaldreifing er stundum kölluð Gauss-dreifing eftir stærðfræðingnum merka Carl Gauss.
Sýnidæmi: Slembispil
Eftirfarandi forrit hermir eftir því að dregið sé spil úr spilastokk. Fyrst er sortin ákvörðuð með því að draga tölu í \(\{0,1,2,3\}\) og svo er dregin tala úr \(\{0,1,2,...,12\}\).
from random import randint
sort = ['hjarta', 'spaða', 'tígul', 'laufa']
nafn = ['ás', 'tvistur', 'þristur', 'fjarki', 'fimma', 'sexa',
'sjöa', 'átta', 'nía', 'tía', 'gosi', 'drottning', 'kóngur']
litur = randint(0, 3)
gildi = randint(0, 12)
spil = sort[litur] + nafn[gildi]
print(spil)
Æfing: Pókerhendur
Afritið forritið að ofan inn í vinnubók og keyrið það nokkrum sinnum. Breytið
svo forritinu í fall, dragaspil() sem skilar streng með dregnu spili.
Búið í framhaldi til forrit sem dregur fimm spil, sem er einmitt fjöldi spila í pókerhönd. Athugið að hér er smá svindl í gangi því það verður möguleiki á að draga sama spil tvisvar. Í kafla 13.4 verður ráðin bót á því.
[Vinnist í samstarfi við kennara.] Búið til fall sem kannar hvort pókerhönd hafi tvær tvennur. Skrifið í famhaldi forrit sem finnur líkurnar á að fá tvær tvennur með hermun (þá eru dregnar margar hendur og athugað hve stórt hlutfall þeirra er hönd með tveim tvennum).
13.2 Slembitölur með NumPy¶
Með NumPy er hægt að búa til slembivigra og slembifylki. Nýjustu útgáfur mæla með að byrjað sé á að skilgreina:
rng = np.random.default_rng()
(rng er skammstöfun á random number generator, slembitölugjafi). Eftir það
má svo nota föllin rng.random, rng.normal og rng.integers til að búa
til slembivigra og -fylki, og reyndar er gott að þekkja líka fallið
rng.uniform sem býr til jafnt dreifðar slembitölur á almennu bili \([a,b]\).
Til að skoða slembivigra og -fylki er hentugt að takmarka fjölda aukastafa með
np.set_printoptions sbr. kafla 10.6.2.
import numpy as np
rng = np.random.default_rng()
np.set_printoptions(suppress=True, precision=3, floatmode="fixed")
x = rng.normal(5, 2, size=8) # 8 normaldreifðar tölur úr N(5,2)
p = rng.integers(0, 2, size=25) # 25 heiltölur, allar 0 eða 1
A = rng.random(size=(2,3)) # 2 x 3 slembifylki, tölur í [0,1]
z = rng.uniform(5, 7, size=10) # 10 jafnt dreifðar tölur í [5,7]
print(x)
print(p)
print(A)
print(z)
Þessi forritsbútur gæti t.d. prentað út:
[4.609 1.920 5.501 5.881 0.098 1.396 4.256 3.368]
[1 0 1 0 1 0 0 1 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0]
[[0.828 0.632 0.758]
[0.355 0.971 0.893]]
[5.230 6.008 6.918 6.901 6.270 5.640 5.465 5.651 6.614 6.931]
Normaldreifðu tölurnar hafa meðaltal 5 og staðalfrávik 2. Svo sjáum við að stiki
númer 2 í rng.integers er einum stærri en stærsta heiltala sem fæst (öfugt
við randint í kafla 13.1).
Æfing:
Afritið sýnidæmið að framan inn í vinnubók og breytið því svo og dragið:
\(4 \times 4\) fylki með tölum úr stöðluðu normaldreifingunni, N(0,1)
vigur með 7 tölum í \(\{2,4,6,\ldots,100\}\)
\(3 \times 3\) fylki með tölum á bilinu \([2,5]\) með
rng.random\(3 \times 3\) fylki með tölum á bilinu \([2,5]\) með
rng.uniform
Í lið 2 eru fyrst búnar til tölur í \(\{1,2,\ldots,50\}\) og niðurstaðan margfölduð með 2, og í lið 3 er fyrst búið til fylki með tölum í \([0,1]\) og svo þarf að margfalda með 3 og leggja 2 við.
13.3 Upphafsstilling slembitalna¶
Það getur komið sér vel að geta stillt slembitölugjafa þannig að það fáist alltaf sama runa af slembitölum þegar forrit er keyrt aftur og aftur. Í random-einingunni er það gert með fallinu seed, t.d. svona:
from random import randint, seed
seed(42)
x = [randint(1,3) for i in range(5)]
print(x)
Þessi bútur prentar alltaf sömu fimm tölurnar, 3, 1, 1, 3, 2 þegar hann er keyrður aftur og aftur, en án seed fengjust alltaf nýjar og nýjar tölur. Fallið default_rng í NumPy hefur valkvæðan stika sem nota má til frumstillingar, svona:
rng = np.random.default_rng(seed=42)
Æfing:
Prófið að keyra forritsbútinn hér á undan með öðru seed, og prófið líka að sleppa frumstillingunni
13.4 Slembiröð og slembiúrtak¶
Í æfingunni „Pókerhendur“ í kafla 13.1 og framhaldi hennar
í verkefni 35 sáum við gagnsemi þess að geta valið af handahófi
úr einhverju safni nokkur stök samtímis. Það er hægt með fallinu sample í
random-einingunni og NumPy býður líka upp á þennan möguleika með fallinu
rng.choice. Bæði random og NumPy eru líka með föll sem bæði heita
shuffle til að umraða lista/vigri í handahófsröð, líkt og þegar spil eru
stokkuð (shuffled). Þriðja aðgerðin sem stundum þarf er að skila tölunum
\(0\) til \(n-1\) í handahófsröð. Í NumPy er sérstakt fall til þess,
permutation, en með random þarf að nota sample. Hér er yfirlit yfir
þessi föll miðað við að L sé listi og x sé vigur:
import numpy as np
from random import sample, shuffle
rng = np.random.default_rng()
H = sample(L, n) # H verður listi með n stökum völdum af handahófi úr L
y = rng.choice(x, n) # y verður vigur mð n stökum völdum af handahófi úr x
shuffle(L) # stokkar listann L
rng.shuffle(x) # stokkar vigurinn x
P = sample(range(n),n) # P verður listi með tölunum 0 til n-1 í slembiröð
p = rng.permutation(n) # p verður vigur með tölunum 0 til n-1 í slembiröð
Æfing: Slembival og sembiröð
Raðið listanum
["Ari", "Ása", "Jói", "Óli", "Una"]í handahófsröð.Veljið þrjá einstaklinga af handahófi úr listanum í lið 1
Lát \(x_k = k + k^2, k = 1,\ldots 5\). Búið til vigur úr þessum x-um með yfirgripi (comprehension) og raðið honum svo í slembiröð.
Gerið ráð fyrir að
spurningsé listi af spurningum ogsvarsé listi af tilsvarandi svörum. Notiðsample(sbr. næstneðstu línuna í töflunni) og yfirgrip til að raða spurningunum í handahófsröð og svörunum í sömu röð. Prófið með:spurning = ["Litur himinsins?", "2+2?", "Hver vann?", "Er sól?"] svar = ["blár", "4", "Jói", "nei"]
13.5 Gervigögn og aðhvarf¶
Eins og sagt var fremst í þessum 13. kafla er ein af hagnýtingum slembitalna sú að búa til gervigögn. Við sáum dæmi um það þegar búin voru til súlurit af normaldreifðum gögnum í 9. kafla. Hér verður skoðað hvernig hægt er að búa til gervigögn til að útskýra jöfnur bestu línu og bestu parabólu, sem unnið er með í verkefni 25, og auk þess jöfnu besta plans. Lesendur ættu að byrja á að skoða verkefni 25
Besta parabóla
Eftirfarandi forritsbútur býr til 100 punkta gervigögn sem mætti lýsa með parabólu sem hefur hágildi nálægt x = 10. Þau eru búin til með því að byrja með nákvæm gildi parabólunnar \(y = 100 - (x - 10)^2\) í x-gildum sem valin eru af handahófi á bilinu \([2,18]\), en svo er bætt við þau normaldreifðri slembiviðbót \(\Delta\) með meðaltal 0 og staðalfrávik 10 (sem rita má \(\Delta \sim N(0,10)\)).
n = 100
x = rng.uniform(2, 18, size=n)
yp = 100 - (x - 10)**2
delta = rng.normal(0, 10, size=n)
y = yp + delta
Hér er svo forrit til að ákvarða bestu parabólu og teikna hana ásamt punktunum. Import- og teiknistillingarskipunum hefur verið sleppt. Myndin sem teiknast fylgir í kjölfarið. Dæmið sýnir hvernig hægt er að fá tvær hlutmyndir hlið við hlið, en á það er líka minnst í verkefni 27. Hágildispunkturinn sem prentaður er út fæst auðveldlega með því að diffra jöfnu parabólunnar og setja sama sem núll.
def plottapunkta(x,y,k):
plt.subplot(1,2,k)
plt.scatter(x, y, s=15, c='darkblue')
plt.xlim(2,18)
plt.grid()
plottapunkta(x,y,1)
plottapunkta(x,y,2)
(a,b,c) = np.polyfit(x, y, deg=2)
X = np.linspace(2, 18, 100)
Y = a*X**2 + b*X + c
plt.plot(X, Y, color='tomato', lw=2.5)
print(f"Stærsta gildið er í x = {-b/(2*a):.1f}")
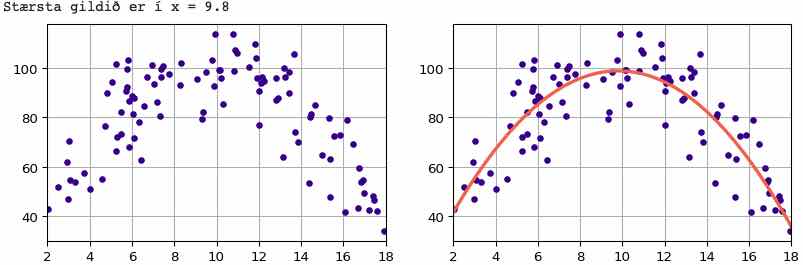
Mynd 13.1: Gervigögn ásamt bestu (minnstu kvaðrata) parabólu¶
Það má hugsa sér allskyns alvörugögn sem þessir punktar gætu lýst. Hér eru örfá dæmi:
Vaxtarhraði plöntu eftir því hvað hún er vökvuð mikið
Suðutími til að fá fullkomin egg að mati 10 manns. Hver þeirra sýður 10 egg í mislangan tíma og gefur útkomunni einkunn.
Heilbrigði eftir magni einhvers mikilvægs hormóns eða vítamíns í blóði.
Fyrir flóknari gögn má líka búa til margliður af hærra stigi.
Æfing: Besta 3. stigs margliða
Búið til 100 punkta gervigögn fyrir fallið \(y = x(x - 2)(x - 4)\) á bilinu \([0,4]\), finnið 3. stigs feril og teiknið hann og gögnin. Hér þarf að nota lægra staðalfrávik á \(\Delta\) en að ofan, t.d. \(\Delta = 0.1\)
Besta lína: Trjávöxtur
Í reitnum hér á eftir eru búin til gervigögn sem gætu lýst hæð 5–15 ára trjáa sem falli af aldri þeirra. Trén hækka um u.þ.b. einn metra á ári. Ef \(h_i\) og \(x_i\) eru hæð og aldur \(i\)-ta trésins þá má nota formúluna:
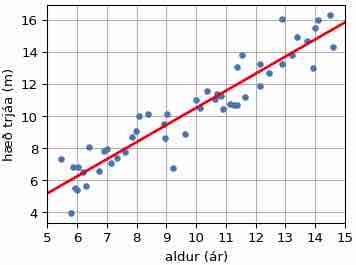
Mynd 13.2: Hæð trjáa eftir aldri¶
aldur = rng.uniform(5,15, size=50)
eps = rng.normal(size = 50)
hæð = 0.5 + 1*aldur + eps
(a,b) = np.polyfit(aldur, hæð, deg=1)
X = np.linspace(5,15)
Y = a*X + b
Hér til hægri er mynd sem gæti komið út úr plt.scatter(aldur, hæð) og plt.plot(X,Y) ásamt nokkrum skipunum til að stilla teikninguna, merkja ása o.fl.
Besta plan: Tré vaxa hægar í fjöllum
Hugsum okkur nú að tré sem vaxa á fjöllum séu lægri en þau sem eru við sjávarmál (sem er ábyggilega rétt), og munurinn sé u.þ.b. 1 m fyrir hverja 100 m sem þau standar hærra í brekkunni (en það er bara skáldskapur). Þá mætti nota formúluna:
þar sem \(h_i\) og \(x_i\) eru hæð og aldur eins og fyrr og \(y_i\)
er hæð yfir sjó. Hér er forritsbútur til að smíða og teikna svona gögn. Aftur
sleppum við ýmsum stillingar- og merkingarskipunum, en höfum samt með clim
sem ekki hefur sést áður og stillir efri og neðri mörk á litaskalanum:
import matplotlib.pyplot as plt
rng = np.random.default_rng(seed=42)
aldur = rng.uniform(5, 15, size=50)
hys = rng.uniform(0, 400, size=50)
eps = rng.normal(0, 1, size=50)
hæð = 0.5 + 1*aldur - 0.01*hys + eps
plt.scatter(aldur, hæð, c=hys)
plt.clim(0,400)
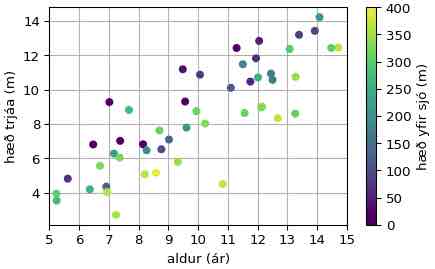
Mynd 13.3: Hæð trjáa eftir aldri og hys¶
Þessum gögnum er hvorki hægt að lýsa með beinni línu eða parabólu heldur þarf plan með formúlu:
Til að finna besta plan af þessu tagi í skilningi minnstu kvaðrata dugar ekki
polyfit heldur þarf annan pakka sem nefnist statsmodels, eins og hér er sýnt:
import statsmodels.api as sm
X = np.array([aldur, hys]).T
X = sm.add_constant(X)
model = sm.OLS(hæð, X) # OLS = ordinary least squares
result = model.fit()
(a,b,c) = result.params
print(f"a={a:.3f}, b={b:.3f}, c={c:.4f}")
# prentar út: a=0.232, b=0.1.020, c=-0.0101
Athugasemd
Ég fékk villumeldingu á import statsmodels.api og þurfti að fara á
skipanalínu og skrifa þar conda install statsmodels (sbr. kafla
3.2 – reyndar bætti ég statsmodels
við upptalninguna í conda install þar þegar ég lenti í þessu).
Æfing: Hæð körfuboltamanna
Búið til línulegt líkan (besta plan) sem lýsir hæð körfuboltamanna í skránni
https://cs.hi.is/python/karfa.txt sem
fall af aldri og þyngd (skráin er með þrjá talnadálka með aldri, hæð og
þyngd, og án hauslínu, og hana má lesa með np.loadtxt). Prentið
niðurstöðu með eftirfarandi sniði:
Módelið er: hæð = 160.x – x.xx*aldur + x.xx*þyngd
Prófið líka að prenta result.summary()
